题目内容
2.△ABC,内角A,B,C所对的边分别是a,b,c,且$\frac{acosB+bcosA}{c}=2cosC$.(1)求角C的大小;
(2)若${S_{△ABC}}=2\sqrt{3}$,a=4,求c.
分析 (1)根据正弦定理可得和两角和正弦公式即可求出答案,
(2)根据三角形的面积公式和余弦定理即可求出.
解答 解:(1)∵$\frac{acosB+bcosA}{c}=2cosC$
∴acosB+bcosA=2ccosC,
由正弦定理得:sinAcosB+sinBcosA=2sinCcosC,
即sin(A+B)=2sinCcosC,
∵0<c<π,
∴sinC>0,
∴$cosC=\frac{1}{2}$,
∴$c=\frac{π}{3}$.
(2)由(1)知$C=\frac{π}{3}$,
∵${S_{△ABC}}=2\sqrt{3}$,
∴$\frac{1}{2}$ab×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$b=2$\sqrt{3}$,
解得b=2.
∴${c^2}={a^2}+{b^2}-2ab×\frac{1}{2}=12$,
∴$c=2\sqrt{3}$.
点评 本题考查了正弦定理和余弦定理和三角形的面积公式以及两角和的正弦公式,考查了学生的运算能力和转化能力,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
12.已知甲、乙两个容器,甲容器容量为x,装满纯酒精,乙容器容量为z,其中装有体积为y的水(x,y<z,单位:L).现将甲容器中的液体倒入乙容器中,直至甲容器中液体倒完或乙容器盛满,搅拌使乙容器中两种液体充分混合,再将乙容器中的液体倒入甲容器中直至倒满,搅拌使甲容器中液体充分混合,如此称为一次操作,假设操作过程中溶液体积变化忽略不计.设经过n(n∈N*)次操作之后,乙容器中含有纯酒精an(单位:L),下列关于数,列{an}的说法正确的是( )
| A. | 当x=y=a时,数列{an}有最大值$\frac{a}{2}$ | |
| B. | 设bn=an+1-an(n∈N*),则数列{bn}为递减数列 | |
| C. | 对任意的n∈N*,始终有${a_n}≤\frac{xy}{z}$ | |
| D. | 对任意的n∈N*,都有${a_n}≤\frac{xy}{x+y}$ |
13.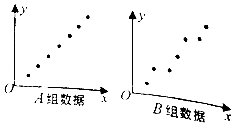 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
 如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )
如图,给出了样本容量均为7的A、B两组样本数据的散点图,已知A组样本数据的相关系数为r1,B组数据的相关系数为r2,则( )| A. | r1>r2>0 | B. | r2>r1>0 | C. | r1<r2<0 | D. | r2<r1<0 |
14.在等差数列{an}中,a3=3,d=2,则a1=( )
| A. | 1 | B. | -1 | C. | 7 | D. | 2 |
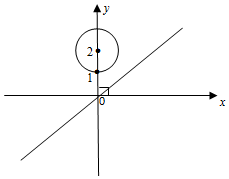 已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线上,过点P作圆M的切线PA,PB,切点为A,B.
已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线上,过点P作圆M的切线PA,PB,切点为A,B.