题目内容
已知x，y满足x=
，则
的取值范围是（ ）
| 3-(y-2)2 |
| y+1 | ||
x+
|
A、[
| ||||||
B、[0，
| ||||||
C、[0，
| ||||||
D、[
|
考点：函数的值域
专题：计算题,函数的性质及应用
分析：x，y满足x=
，即x2+（y-2）2=3（x≥0），表示以（0，2）为圆心，
为半径的上半圆，利用斜率，即可求出
的取值范围．
| 3-(y-2)2 |
| 3 |
| y+1 | ||
x+
|
解答：
解：x，y满足x=
，即x2+（y-2）2=3（x≥0），表示以（0，2）为圆心，
为半径的右半圆，
∵（0，2+
）与（-
，-1）连线的斜率为
=
+1，直线y+1=k（x+
）与半圆相切时，k=
∴
的取值范围是[
，
+1]，
故选：D．
| 3-(y-2)2 |
| 3 |
∵（0，2+
| 3 |
| 3 |
3+
| ||
|
| 3 |
| 3 |
| ||
| 3 |
∴
| y+1 | ||
x+
|
| ||
| 3 |
| 3 |
故选：D．
点评：本题考查
的取值范围，考查学生分析解决问题的能力，转化为求斜率是关键．
| y+1 | ||
x+
|
练习册系列答案
相关题目
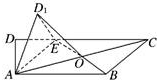如图，在梯形ABCD中，AB∥CD，∠ADC=90°，AB=2，DC=3，AD=1．E是DC上一点，且DE=1，连接AE，将△DAE沿AE折起到△D1AE的位置，使得∠D1AB=30°，设AC与BE的交点为O．