题目内容
已知O为原点,A(x1,y1),B(x2,y2)是椭圆C:
+
=1(m>4)上任意两点,向量
=(x1,
),
=(x2,
),若p,q的夹角为
且椭圆的离心率e=
,求△AOB的面积是否为定值?
| x2 |
| m |
| y2 |
| 4 |
| p |
| y1 |
| 2 |
| q |
| y2 |
| 2 |
| π |
| 2 |
| ||
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由椭圆方程结合椭圆的离心率求得m的值,再由
=(x1,
),
=(x2,
)且
•
=0得到
x1x2+
=0,首先分析直线AB的斜率存在时,设出直线方程,和椭圆方程联立,利用根与系数关系得到A,B两点横纵坐标的乘积,代入x1x2+
=0得到直线AB的斜率和截距的关系,然后写出△AOB的面积,最后结果不能把变量消掉,说明△AOB的面积不是定值.
| p |
| y1 |
| 2 |
| q |
| y2 |
| 2 |
| p |
| q |
x1x2+
| y1y2 |
| 4 |
| y1y2 |
| 4 |
解答:
解:由椭圆
+
=1(m>4),得b=2,
∵e=
=
,
∴
=
=1-
=
,则a2=16,即m=16.
∴椭圆的方程为
+
=1.
向量
=(x1,
),
=(x2,
),
由
,
的夹角为
,得
•
=0,即x1x2+
=0,
当直线AB斜率存在时,设直线AB方程为:y=kx+m,
联立
,消去y得(1+4k2)x2+8kmx+4m2-16=0,
∴△=64k2m2-4(1+4k2)(4m2-16)>0,
x1+x2=-
,x1x2=
,
∴4x1x2+y1y2=4x1x2+(kx1+m)(kx2+m)
=(4+k2)x1x2+km(x1+x2)+m2=0,
即(4+k2)•
-
+m2=0,
化简得17m2-16k2-64=0,
S△AOB=
|-
||y1-y2|
=
|m||x1-x2|
=
|m|
=
|m|
=16|m|•
.不是定值.
| x2 |
| m |
| y2 |
| 4 |
∵e=
| c |
| a |
| ||
| 2 |
∴
| c2 |
| a2 |
| a2-b2 |
| a2 |
| b2 |
| a2 |
| 3 |
| 4 |
∴椭圆的方程为
| x2 |
| 16 |
| y2 |
| 4 |
向量
| p |
| y1 |
| 2 |
| q |
| y2 |
| 2 |
由
| p |
| q |
| π |
| 2 |
| p |
| q |
| y1y2 |
| 4 |
当直线AB斜率存在时,设直线AB方程为:y=kx+m,
联立
|
∴△=64k2m2-4(1+4k2)(4m2-16)>0,
x1+x2=-
| 8km |
| 1+4k2 |
| 4m2-16 |
| 1+4k2 |
∴4x1x2+y1y2=4x1x2+(kx1+m)(kx2+m)
=(4+k2)x1x2+km(x1+x2)+m2=0,
即(4+k2)•
| 4m2-16 |
| 1+4k2 |
| 8k2m2 |
| 1+4k2 |
化简得17m2-16k2-64=0,
S△AOB=
| 1 |
| 2 |
| m |
| k |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
=
| 1 |
| 2 |
| ||
| 1+4k2 |
=16|m|•
| ||
| 17m2-60 |
点评:本题考查了椭圆的简单几何性质,考查了平面向量在解题中的应用,考查了计算能力,是压轴题.

练习册系列答案
相关题目
已知x,y满足x=
,则
的取值范围是( )
| 3-(y-2)2 |
| y+1 | ||
x+
|
A、[
| ||||||
B、[0,
| ||||||
C、[0,
| ||||||
D、[
|
函数f(x)的定义域为全体实数,f(-1)=2,对任意x∈R,f′(x)>1,则f(x)>x+3的解集为( )
| A、(1,1) |
| B、(-1,+∞) |
| C、(-∞,-1) |
| D、R |
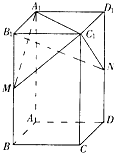 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.