题目内容
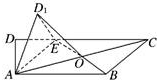 如图,在梯形ABCD中,AB∥CD,∠ADC=90°,AB=2,DC=3,AD=1.E是DC上一点,且DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=30°,设AC与BE的交点为O.
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,AB=2,DC=3,AD=1.E是DC上一点,且DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=30°,设AC与BE的交点为O.(1)试用基向量
| AB |
| AE |
| AD1 |
| CD1 |
(2)求异面直线OD1与BC所成角的余弦值.
考点:异面直线及其所成的角,平面向量数量积的运算
专题:平面向量及应用
分析:(1)根据向量的基本定理即可得到结论.
(2)设异面直线OD1与BC所成的角为θ,然后根据向量的夹角公式即可.
(2)设异面直线OD1与BC所成的角为θ,然后根据向量的夹角公式即可.
解答:
解:(1)
=
+
=
-
+
-
=-
-
-
(2)设异面直线OD1与BC所成角的θ,
则cosθ=|cos<
,
>|=|cos<
,
>|=|
|
∵
•
=(
-
-
)•
=
•
-
•
-
2=1×
×cos45°-
×2×
×cos45°-
×(
)2=-1,
|
|=
=
,
则cosθ=|cos<
,
>|=|
|=
=
故异面直线OD1与BC所成角的余弦值是
.
| CD1 |
| CE |
| ED1 |
| AE |
| AC |
| AD1 |
| AE |
| AE |
| AB |
| AD1 |
(2)设异面直线OD1与BC所成角的θ,
则cosθ=|cos<
| OD1 |
| AE |
| OD1 |
| BC |
| ||||
|
|
∵
| OD1 |
| OE |
| AD1 |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AE |
| AE |
| AD1 |
| AE |
| 1 |
| 2 |
| AB |
| AE |
| 1 |
| 2 |
| AE |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
|
| OD1 |
(
|
| ||
| 2 |
则cosθ=|cos<
| OD1 |
| BC |
| ||||
|
|
| 1 | ||||||
|
| ||
| 3 |
故异面直线OD1与BC所成角的余弦值是
| ||
| 3 |
点评:本题主要考查异面直线所成角的求解,利用向量法是解决本题的关键.

练习册系列答案
相关题目
圆柱的轴截面ABCD是边长为2的正方形,M为正方形ABCD的对角线的交点,动点P在圆柱下底面内(包括圆周),若直线AM与直线MP所成的角为45°,则点P形成的轨迹为( )
| A、椭圆的一部分 |
| B、抛物线的一部分 |
| C、双曲线的一部分 |
| D、圆的一部分 |
已知x,y满足x=
,则
的取值范围是( )
| 3-(y-2)2 |
| y+1 | ||
x+
|
A、[
| ||||||
B、[0,
| ||||||
C、[0,
| ||||||
D、[
|

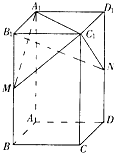 如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别是棱BB1,DD1的中点.