题目内容
在△ABC中,已知sinB+sinC=sinA(cosB+cosC).
(1)判断△ABC的形状;
(2)若角A所对的边a=1,试求△ABC内切圆半径的取值范围.
(1)判断△ABC的形状;
(2)若角A所对的边a=1,试求△ABC内切圆半径的取值范围.
考点:三角形的形状判断
专题:计算题,解三角形
分析:(1)由已知等式利用正、余弦定理,化简,即可判断△ABC的形状;
(2)由△ABC为直角三角形,知内切圆半径r=
,利用角A所对的边a=1,结合三角函数,即可求△ABC内切圆半径的取值范围.
(2)由△ABC为直角三角形,知内切圆半径r=
| b+c-a |
| 2 |
解答:
解:(1)由已知等式利用正、余弦定理得b+c=a(
+
),…(3分)
整理得(b+c)(b2+c2-a2)=0,
∴b2+c2=a2,
∴△ABC为直角三角形,且∠A=90°. …(6分)
(2)由△ABC为直角三角形,
知内切圆半径r=
=
(sinB+sinC-1)=
(sinB+cosB-1),…(11分)
∵sinB+cosB=
sin(B+
)≤
,
∴0<r≤
. …(14分)
| a2+c2-b2 |
| 2ac |
| a2+b2-c2 |
| 2ab |
整理得(b+c)(b2+c2-a2)=0,
∴b2+c2=a2,
∴△ABC为直角三角形,且∠A=90°. …(6分)
(2)由△ABC为直角三角形,
知内切圆半径r=
| b+c-a |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵sinB+cosB=
| 2 |
| π |
| 4 |
| 2 |
∴0<r≤
| ||
| 2 |
点评:本题考查三角形的形状判断,考查正、余弦定理,考查辅助角公式,考查学生的计算能力,属于中档题.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
若△ABC三个内角A、B、C的对边分别为a,b,c,且a=1,∠B=45°,S△ABC=2,则sinA=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
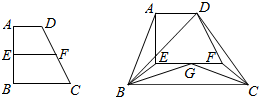 如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4.点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.
如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4.点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.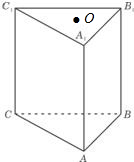 如图,三棱柱ABC-A1B1C1的棱长为1,上底面△A1B1C1的中心为O,若有一只蚂蚁从A点出发到O点取食再回到A点(不走回头路),则蚂蚁走过的最短路程为
如图,三棱柱ABC-A1B1C1的棱长为1,上底面△A1B1C1的中心为O,若有一只蚂蚁从A点出发到O点取食再回到A点(不走回头路),则蚂蚁走过的最短路程为