题目内容
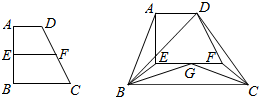 如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4.点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.
如图,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4.点E,F分别是AB,CD的中点,点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.(Ⅰ)当EG=2时,求证:CG⊥平面BDG.
(Ⅱ)在线段EF上任意取一点,当该点落在线段EG上的概率为
| 1 |
| 3 |
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间角
分析:(Ⅰ)由已知条件推导出AEGD为为正方形,DG⊥EF,从而得到DG⊥CG,由此利用勾股定理能证明CG⊥面BDG.
(Ⅱ)建立空间坐标系E-xyz,利用向量法能求出此二面角平面角的余弦值.
(Ⅱ)建立空间坐标系E-xyz,利用向量法能求出此二面角平面角的余弦值.
解答:
(Ⅰ)证明:∵EG=2,直角梯形ABCD中,∠ABC=90°,
AB=BC=2AD=4.点E,F分别是AB,CD的中点,
点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.
∴AEGD为为正方形,∴DG⊥EF,
∵平面AEFD⊥平面EBCF,∴DG⊥平面EBCF,∴DG⊥CG,
又∵EG=EB=2.∴BG=CG=2
,
由BG2+CG2=BC2,知BG⊥CG,BG∩DG=G,
∴CG⊥面BDG.…(6分)
(Ⅱ)解:点E、F分别是AB的中点,
∴EF∥BC,又∠ABC=90°,∴AE⊥EF,
∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
如图建立空间坐标系E-xyz.
由题意得B(2,0,0),D(0,2,2)C(2,4,0),G(0,1,0),
设平面DBG的法向量为
=(x,y,z),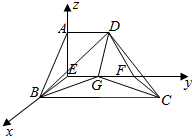
∴
=(-2,1,0),
=(-2,2,2),…(7分)
则
,即
取x=1,则y=2,z=-1,∴
=(1,2,-1)…(9分)
取面BCG的一个法向量为
=(0,0,1).
则cos<
,
>=
=-
…(10分)
∴此二面角平面角的余弦值为
.…(12分)
AB=BC=2AD=4.点E,F分别是AB,CD的中点,
点G在EF上,沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCD.
∴AEGD为为正方形,∴DG⊥EF,
∵平面AEFD⊥平面EBCF,∴DG⊥平面EBCF,∴DG⊥CG,
又∵EG=EB=2.∴BG=CG=2
| 2 |
由BG2+CG2=BC2,知BG⊥CG,BG∩DG=G,
∴CG⊥面BDG.…(6分)
(Ⅱ)解:点E、F分别是AB的中点,
∴EF∥BC,又∠ABC=90°,∴AE⊥EF,
∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
如图建立空间坐标系E-xyz.
由题意得B(2,0,0),D(0,2,2)C(2,4,0),G(0,1,0),
设平面DBG的法向量为
| n1 |

∴
| BG |
| BD |
则
|
|
取x=1,则y=2,z=-1,∴
| n |
取面BCG的一个法向量为
| n2 |
则cos<
| n1 |
| n2 |
| ||||
|
| ||
| 6 |
∴此二面角平面角的余弦值为
| ||
| 6 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=
如图所示,PA⊥平面ABCD,ABCD是矩形,AB=1,AD=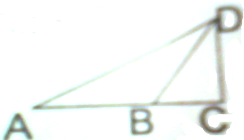 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100