题目内容
如果圆x2+y2=3n2至少覆盖函数f(x)=
sin
的两个最大值点和两个最小值点,则正整数n的最小值为 .
| 3 |
| πx |
| n |
考点:函数y=Asin(ωx+φ)的图象变换,圆的标准方程
专题:直线与圆
分析:先用R表示出周期,得到最大值点和最小值点的坐标后,代入到圆的方程可求出R的值,最后可得答案.
解答:
解:∵x2+y2=n2,∴x∈[-n,n].
∵函数f(x)的最小正周期为2n,∴最大值点为(
,
),相邻的最小值点为(-
,-
),
∵圆x2+y2=n2至少覆盖函数f(x)=
sin
的一个最大值点和一个最小值点,
∴
+3≤n2,解得n≥2.∵n∈N,∴n=2.
故答案为:2.
∵函数f(x)的最小正周期为2n,∴最大值点为(
| n |
| 2 |
| 3 |
| n |
| 2 |
| 3 |
∵圆x2+y2=n2至少覆盖函数f(x)=
| 3 |
| πx |
| n |
∴
| n2 |
| 4 |
故答案为:2.
点评:本题主要考查三角函数的周期性,利用了三角函数两相邻的最大值与最小值正好等于半个周期,属于中档题.

练习册系列答案
相关题目
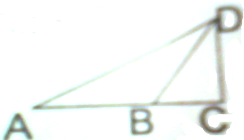 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100