题目内容
在(
+
)20的展开式中,x的幂指数是整数的项共有( )
| 3 | x |
| 1 | ||
|
| A、3项 | B、4项 | C、5项 | D、6项 |
考点:二项式系数的性质
专题:二项式定理
分析:求出展开式的通项公式,即可求出x的幂指数是整数的项的个数.
解答:
解:展开式的通项公式为Tk+1=
?(
)20-k?(
)k=
?x
-
=
?x
,
要使,x的幂指数是整数,
则40-5k必须是6的整数倍,
∴当k=2时,
=
=5,满足条件.
当k=8时,
=0,满足条件.
当k=14时,
=
=-
=-5,满足条件.
当k=20时,
=
=-
=-10,满足条件.
即x的幂指数是整数的项共有4项,
故选:B.
| C | k 20 |
| 3 | x |
| 1 | ||
|
| C | k 20 |
| 20-k |
| 3 |
| k |
| 2 |
| C | k 20 |
| 40-5k |
| 6 |
要使,x的幂指数是整数,
则40-5k必须是6的整数倍,
∴当k=2时,
| 40-5k |
| 6 |
| 30 |
| 6 |
当k=8时,
| 40-5k |
| 6 |
当k=14时,
| 40-5k |
| 6 |
| 40-70 |
| 6 |
| 30 |
| 6 |
当k=20时,
| 40-5k |
| 6 |
| 40-100 |
| 6 |
| 60 |
| 6 |
即x的幂指数是整数的项共有4项,
故选:B.
点评:本题主要考查二项式定理的应用,根据条件求出展开式的通项公式是解决二项式定理的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
设集合A={y|y=x2-2x},B={x|y=log2(3-x),则A∩B=( )
| A、∅ | B、(-1,3) |
| C、[-1,3) | D、[-1,3] |
点A(a,6)到直线3x-4y=2的距离d=4,则a=( )
A、
| ||
B、-
| ||
| C、-2 | ||
D、
|
已知集合A={x||x|>1},B={x|x2+x-6≤0},则集合A∩B=( )
| A、{x|-3≤x<-1或1<x≤2} |
| B、{x|-3≤x<-1或x>1} |
| C、{x|-3≤x<-1或1≤x<2} |
| D、{x|x<-3或1<x≤2} |
已知复数z=(x-1)+(2x-1)i的模小于
,则实数x的取值范围是( )
| 10 |
A、-
| ||
| B、x<2 | ||
C、x>-
| ||
D、x>2或x<-
|
直线l1:x+ay+1=0与l2:(a-3)x+2y-5=0(a∈R)互相垂直,则直线l2的斜率为( )
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
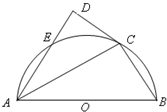 (平面几何选做题)
(平面几何选做题)