题目内容
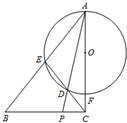 如图,△ABC中,∠ACB=90°,以边AC上的点O为圆心,OA为半径作圆,与边AB,AC分别交于点E,F,EC与⊙O交于点D,连结AD并延长交BC于P,已知AE=EB=4,AD=5,求AP的长.
如图,△ABC中,∠ACB=90°,以边AC上的点O为圆心,OA为半径作圆,与边AB,AC分别交于点E,F,EC与⊙O交于点D,连结AD并延长交BC于P,已知AE=EB=4,AD=5,求AP的长.考点:与圆有关的比例线段
专题:选作题,立体几何
分析:证明B,C,F,E四点共圆、B,P,D,E四点共圆,可得AE•AB=AD•AP,即可求AP的长.
解答:
 解:连接EF,则∠AEF=90°,
解:连接EF,则∠AEF=90°,
∵∠ACB=90°,
∴B,C,F,E四点共圆,
∴∠AFE=∠B,
∵∠ADE=∠AFE,
∴∠ADE=∠B,
∴B,P,D,E四点共圆,
∴AE•AB=AD•AP
∵AE=EB=4,AD=5,
∴AP=
.
 解:连接EF,则∠AEF=90°,
解:连接EF,则∠AEF=90°,∵∠ACB=90°,
∴B,C,F,E四点共圆,
∴∠AFE=∠B,
∵∠ADE=∠AFE,
∴∠ADE=∠B,
∴B,P,D,E四点共圆,
∴AE•AB=AD•AP
∵AE=EB=4,AD=5,
∴AP=
| 32 |
| 5 |
点评:本题考查四点共圆,考查切割线定理的运用,证明B,P,D,E四点共圆是关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知函数f(x)=sinxcosx,则f(x)是( )
| A、奇函数 |
| B、偶函数 |
| C、非奇非偶函数 |
| D、既是奇函数又是偶函数 |
若z∈C且|z+2-2i|=1,则|z-1-2i|的最小值是( )
| A、2 | B、3 | C、4 | D、5 |
按图所示的程序框图运算:若输出k=2,则输入x的取值范围是( )


| A、(20,25] |
| B、(30,32] |
| C、(28,57] |
| D、(30,57] |
将4个不同的小球放入3个不同的盒中,每个盒子至少放入一球,则不同方法为( )
| A、81 | B、36 | C、64 | D、24 |
 如图,三棱柱ABC-A1B1C1中,BC=2,BC1=
如图,三棱柱ABC-A1B1C1中,BC=2,BC1=