题目内容
若z∈C且|z+2-2i|=1，则|z-1-2i|的最小值是（ ）
| A、2 | B、3 | C、4 | D、5 |
考点：复数求模
专题：数系的扩充和复数
分析：根据两个复数差的几何意义，求得|z-1-2i|的最小值．
解答：
解：∵|z+2-2i|=1，∴复数z对应点在以C（-2，2）为圆心、以1为半径的圆上．
而|z-1-2i|表示复数z对应点与点A（1，2）间的距离，
故|z-1-2i|的最小值是|AC|-1=2，
故选：A．
而|z-1-2i|表示复数z对应点与点A（1，2）间的距离，
故|z-1-2i|的最小值是|AC|-1=2，
故选：A．
点评：本题主要考查两个复数差的几何意义，求复数的模的最值，属于基础题．
练习册系列答案
相关题目
如果-1，m、n、p、-16成等比数列，那么（ ）
| A、n=-4，mp=-16 |
| B、n=-4，mp=16 |
| C、n=4，mp=16 |
| D、n=4，mp=-16 |
对于二项式（1-x）1999，有下列四个命题正确的是（ ）
A、展开式中T1000=C
| ||
| B、展开式中非常数项系数和是1 | ||
| C、展开式中系数最大的项是第1000项和第1001项 | ||
| D、当x=2000时，（1-x）1999除以2000的余数是1 |
已知sin（
+α）=
，则cos（
+α）的值为（ ）
| π |
| 3 |
| 4 |
| 5 |
| 5π |
| 6 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
sin570°=（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
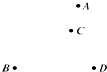如图A、B、C、D是某油田的四口油井，计划建三条路，将这四口油井连结起来（每条路只连结两口油井），那么不同的建路方案有（ ）| A、12种 | B、14种 |
| C、16种 | D、18种 |
在复平面上复数i，1，4+2i所对应的点分别是A、B、C，则平行四边形ABCD的对角线BD的长为（ ）
| A、5 | ||
B、
| ||
C、
| ||
D、
|
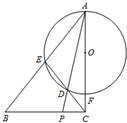如图，△ABC中，∠ACB=90°，以边AC上的点O为圆心，OA为半径作圆，与边AB，AC分别交于点E，F，EC与⊙O交于点D，连结AD并延长交BC于P，已知AE=EB=4，AD=5，求AP的长．