题目内容

已知f（x）=
x
，p，q＞0，且p+q=1，求证：pf（x1）+qf（x2）≤f（px1+qx2）．
考点：综合法与分析法(选修）
专题：证明题,不等式的解法及应用
分析：根据函数关系，利用分析法证明即可．
解答： 证明：若证pf（x1）+qf（x2）≤f（px1+qx2），
只需证p
x1
+q
x2
≤
px1+qx2
，
只需证p2x1+q2x2+2pq
x1x2
≤px1+qx2，
只需证px1(p-1)+qx2(q-1)+2pq
x1x2
≤0，
只需证-pqx1-pqx2+2pq
x1x2
≤0，
只需证pq(x1+x2-2
x1x2
)≥0，
只需证pq(
x1
-
x2
)2≥0，上式显然成立，
所以原不等式成立．
点评：本题考查分析法，考查学生分析解决问题的能力，掌握分析法的步骤是关键．
练习册系列答案
相关题目
已知sin（
π
3
+α）=
4
5
，则cos（
5π
6
+α）的值为（　　）
A、-
3
5
B、
3
5
C、-
4
5
D、
4
5
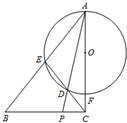如图，△ABC中，∠ACB=90°，以边AC上的点O为圆心，OA为半径作圆，与边AB，AC分别交于点E，F，EC与⊙O交于点D，连结AD并延长交BC于P，已知AE=EB=4，AD=5，求AP的长．
在△ABC中，角A，B，C的对边分别为a，b，c，若a+c=
2
b．
（1）求证：B≤
π
2
；
（2）当
AB
•
BC
=-2，b=2
3
时，求△ABC的面积．
（理）定义区间（c，d），[c，d），（c，d]，[c，d]的长度均为d-c，其中d＞c．
（1）已知函数y=|2x-1|的定义域为[a，b]，值域为[0，
1
2
]，写出区间[a，b]长度的最大值与最小值．
（2）已知函数fM（x）的定义域为实数集D=[-2，2]，满足fM（x）=
x，x∈M
-x，x∈M
（M是D的非空真子集）．集合A=[1，2]，B=[-2，-1]，求F（x）=
fA∪B(x)
fA(x)+fB(x)+3
的值域所在区间长度的总和．
（3）定义函数f（x）=
1
x-1
+
2
x-2
+
3
x-3
+
4
x-4
-1，判断函数f（x）在区间（2，3）上是否有零点，并求不等式f（x）＞0解集区间的长度总和．
已知函数f（x）=ex，g（x）=ax2（a∈R，a≠0）．
（1）求函数y=
g(x)
f(x)
的单调区间；
（2）①已知A（x1，y1），B（x2，y2）（x1＜x2）为函数y=g（x）图象上的两点，y=g′（x）为y=g（x）的导函数，若g′（x0）=
y1-y2
x1-x2
，求证：x0∈（x1，x2）；
②类比函数y=g（x），①中的结论在函数y=f（x）中是否成立？若成立，请给出证明；若不成立，请说明理由．
在数列{an}中，已知a1=1，a2=3，设Sn为数列{an}的前n项和，对于任意的n≥2，n∈N，Sn+1+Sn-1=2（Sn+1）都成立．
（1）求数列{an}的通项公式；
（2）设Tn为数列{
1
anan+1
}的前n项和，若Tn≤λan+1对n∈N*恒成立，求实数λ的取值范围．
由两个四棱锥组合而成的空间几何体的三视图如图所示，其体积是
 
；表面积是
 
．
路灯距地平面为8m，一个身高为1.75m的人以
5
7
m/s的速率，从路灯在地面上的射影点C处，沿某直线离开路灯，那么人影长度的变化速率v为
 
m/s．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网