题目内容
已知数列{an}的前n项和为Sn,满足Sn=
an-n.
(Ⅰ)求证:数列{an+1}是等比数列;
(Ⅱ)令bn=log3(a1+1)+log3(a2+1)+…+log3(an+1),则对任意n∈N*,是否存在正整数m,使
+
+…+
≥
都成立?若存在,求出m的值;若不存在,请说明理由.
| 3 |
| 2 |
(Ⅰ)求证:数列{an+1}是等比数列;
(Ⅱ)令bn=log3(a1+1)+log3(a2+1)+…+log3(an+1),则对任意n∈N*,是否存在正整数m,使
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m |
| 4 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)根据条件结合等比数列的定义,利用构造法即可证明数列{an+1}是等比数列;
(Ⅱ)利用裂项法求出bn,然后利用数列和不等式之间的大小关系即可得到结论.
(Ⅱ)利用裂项法求出bn,然后利用数列和不等式之间的大小关系即可得到结论.
解答:
解:(Ⅰ)当n=1,a1=S1=
a1-1,即a1=2,
当n≥2时,由Sn=
an-n.得Sn-1=
an-1-n+1.
两式相减得Sn-Sn-1=
an-
an-1-1=an-1.
即an=3an-1+2,
则an+1=3(an-1+1),
即数列{an+1}是公比q=3的等比数列,首项为a1+1=3.
(Ⅱ)由(Ⅰ)得an+1=3•3n-1=3n,
则log3(an+1)=log33n=n,
即bn=log3(a1+1)+log3(a2+1)+…+log3(an+1)=1+2+…+n=
,
则
=
=2(
-
),
则
+
+…+
=2(1-
+
-
+…
-
)=2(1-
),
若
+
+…+
≥
都成立,
则2(1-
)≥
都成立,
即m≤8(1-
)对任意正整数n都成立.
∵1-
≥1-
=
,
∴m≤4,
即m=1,2,3,4.
| 3 |
| 2 |
当n≥2时,由Sn=
| 3 |
| 2 |
| 3 |
| 2 |
两式相减得Sn-Sn-1=
| 3 |
| 2 |
| 3 |
| 2 |
即an=3an-1+2,
则an+1=3(an-1+1),
即数列{an+1}是公比q=3的等比数列,首项为a1+1=3.
(Ⅱ)由(Ⅰ)得an+1=3•3n-1=3n,
则log3(an+1)=log33n=n,
即bn=log3(a1+1)+log3(a2+1)+…+log3(an+1)=1+2+…+n=
| n(n+1) |
| 2 |
则
| 1 |
| bn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
若
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| bn |
| m |
| 4 |
则2(1-
| 1 |
| n+1 |
| m |
| 4 |
即m≤8(1-
| 1 |
| n+1 |
∵1-
| 1 |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
∴m≤4,
即m=1,2,3,4.
点评:本题主要考查等比数列的通项公式,利用裂项法求前n项和的应用,考查数列与不等式的应用,综合性较强,运算量较大.

练习册系列答案
相关题目
已知圆的方程是(x-2)2+(y-3)2=4,则点P(-3,-2)满足( )
| A、是圆心 | B、在圆上 |
| C、在圆内 | D、在圆外 |
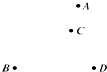 如图A、B、C、D是某油田的四口油井,计划建三条路,将这四口油井连结起来(每条路只连结两口油井),那么不同的建路方案有( )
如图A、B、C、D是某油田的四口油井,计划建三条路,将这四口油井连结起来(每条路只连结两口油井),那么不同的建路方案有( )| A、12种 | B、14种 |
| C、16种 | D、18种 |
数列{an}中,a1=3,a2=6,an+2=an+1-an,那么a6=( )
| A、-2 | B、-3 | C、-6 | D、-8 |
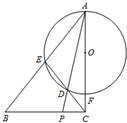 如图,△ABC中,∠ACB=90°,以边AC上的点O为圆心,OA为半径作圆,与边AB,AC分别交于点E,F,EC与⊙O交于点D,连结AD并延长交BC于P,已知AE=EB=4,AD=5,求AP的长.
如图,△ABC中,∠ACB=90°,以边AC上的点O为圆心,OA为半径作圆,与边AB,AC分别交于点E,F,EC与⊙O交于点D,连结AD并延长交BC于P,已知AE=EB=4,AD=5,求AP的长.