题目内容
如图关于星星的图案构成一个数列{an},an(n∈N*)对应图中星星的个数.

(1)写出a5,a6的值及数列{an}的通项公式;
(2)若数列{
}的前n项和Sn,求证Sn<2;
(3)若bn=
,对于(2)中的Sn,有cn=Sn•bn,求数列{|cn|}的前n项和Tn.

(1)写出a5,a6的值及数列{an}的通项公式;
(2)若数列{
| 1 |
| an |
(3)若bn=
| 2n2-9n-11 |
| 2n |
考点:数列的求和,归纳推理
专题:等差数列与等比数列
分析:(1)由图的规律求出a5,a6的值及数列{an}的通项公式;
(2)由(1)求出
=
,再进行裂项,利用裂项相消法求出前n项和Sn,化简后证明不等式成立;
(3)由(2)化简Sn,代入cn=Sn•bn进行因式分解,由通项公式判断出是等差数列,再由前n项和公式求数列{cn}的前n项和Tn′,根据正负项对n分类后,分别去到绝对值后,利用和Tn′求出数列{|cn|}的前n项和Tn.
(2)由(1)求出
| 1 |
| an |
| 2 |
| n(n+1) |
(3)由(2)化简Sn,代入cn=Sn•bn进行因式分解,由通项公式判断出是等差数列,再由前n项和公式求数列{cn}的前n项和Tn′,根据正负项对n分类后,分别去到绝对值后,利用和Tn′求出数列{|cn|}的前n项和Tn.
解答:
解:(1)由图得,a5=1+2+3+4+5=15,a6=1+2+3+4+5+6=21,
所以an=1+2+3+…+n=
;
证明:(2)由(1)得,
=
=2(
-
),
则Sn=2[(1-
)+(
-
)+…+(
-
)]=2(1-
)=2-
又n∈N*,所以Sn<2;
解:(3)由(2)得Sn=2-
=
,
由题意得,cn=Sn•bn=
•
=
=2n-11,
则数列{cn}是以2为公差、以-9为首项的等差数列,
所以数列{cn}的前n项和Tn′=c1+c2+…+cn=
=n2-10n,
①当1≤n≤5时,Tn=|c1|+|c2|+…+|cn|=-(c1+c2+…+cn)=-n2+10n,
②当n≥6时,Tn=|c1|+|c2|+…+|cn|
=-(c1+c2+…+c5)+(c6+c7+…+cn)
=-T5′+Tn′-T5′=-2T5′+Tn′=n2-10n+50,
综上得,Tn=
.
所以an=1+2+3+…+n=
| n(n+1) |
| 2 |
证明:(2)由(1)得,
| 1 |
| an |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
则Sn=2[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2 |
| n+1 |
又n∈N*,所以Sn<2;
解:(3)由(2)得Sn=2-
| 2 |
| n+1 |
| 2n |
| n+1 |
由题意得,cn=Sn•bn=
| 2n |
| n+1 |
| 2n2-9n-11 |
| 2n |
| (2n-11)(n+1) |
| n+1 |
则数列{cn}是以2为公差、以-9为首项的等差数列,
所以数列{cn}的前n项和Tn′=c1+c2+…+cn=
| n(-9+2n-11) |
| 2 |
①当1≤n≤5时,Tn=|c1|+|c2|+…+|cn|=-(c1+c2+…+cn)=-n2+10n,
②当n≥6时,Tn=|c1|+|c2|+…+|cn|
=-(c1+c2+…+c5)+(c6+c7+…+cn)
=-T5′+Tn′-T5′=-2T5′+Tn′=n2-10n+50,
综上得,Tn=
|
点评:本题考查等差数列的通项公式、前n项和公式,裂项相消法求数列的和,以及分类讨论思想,归纳推理,比较综合.

练习册系列答案
相关题目
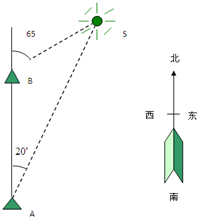 如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
如图,一艘船以32.2n mile/h的速度向正北航行.在A处看灯塔S在船的北偏东20°的方向,30min后航行到B处,在B处看灯塔在船的北偏东65°的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?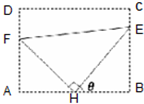 如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10
如图:某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,EF分别落在线段BC,AD上.已知AB=20米,AD=10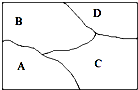 如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有
如图,要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同的颜色,不同的涂色方案有