题目内容

函数f（x）在定义域R上是减函数．若f（2a）＜f（a+3），则实数a的取值范围为
 
．
考点：函数单调性的性质
专题：函数的性质及应用
分析：由条件利用函数的单调性的定义可得2a＞a+3，由此求得a的范围．
解答： 解：由于函数f（x）在定义域R上是减函数，f（2a）＜f（a+3），
∴2a＞a+3，求得a＞3，
故答案为：（3，+∞）．
点评：本题主要考查函数的单调性的定义，属于基础题．
练习册系列答案
相关题目
己知曲线C1：y=-x2+1（y≤0）与x轴交于A，B两点，点P为x轴上方的一个动点，点P与A，B连线的斜率之积为-4
（Ⅰ）求动点P的轨迹C2的方程；
（Ⅱ）过点B的直线l与C1，C2分别交于点M，Q（均异于点A，B），若以MQ为直径的圆经过点A，求△AMQ的面积．
（ax-
3
6
）3的展开式中含x2项的系数为-
3
2
，则∫-2ax2dx的值为
 
．
已知函数f（x）=|x-a|．
（1）若不等式f（x）≤3的解集为{x|-1≤x≤5}，求实数a的值；
（2）在 （1）的条件下，若存在x∈R使得f（x）+f（x+5）≤m成立，求实数m的取值范围．
若f（g（x））=9x+3，g（x）=3x+1，则f（x）的解析式为（　　）
A、3xB、3
C、27x+10D、27x+12
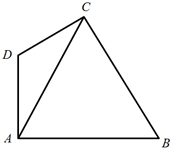某游乐园拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区域ABC为主题活动园区，∠ACB=60°；AD、CD为游客通道（不考虑宽度），通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．
（Ⅰ）若AC=20m，BC=24m，求AB的长度．
（Ⅱ）如图，AB=24m，AD与AB垂直，且∠ADC=120°，∠ABC=θ（45°≤θ≤60°）．记游客通道长度和为L，写出L关于θ的关系式，并求L的最小值．
设a=log022，b=log0.23，c=20.2，d=0.22，则这四个数的大小关系（从小到大排列）是
 
．
（a+2x）5的展开式中，x2的系数等于40，则a等于
 
．
下列函数中，与函数y=x3的奇偶性、单调性均相同的是（　　）
A、y=ex
B、y=2x-
1
2x
C、y=ln|x|
D、y=tanx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网