题目内容
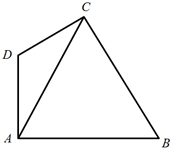某游乐园拟建一主题游戏园，该游戏园为四边形区域ABCD，其中三角形区域ABC为主题活动园区，∠ACB=60°；AD、CD为游客通道（不考虑宽度），通道AD、CD围成三角形区域ADC为游客休闲中心，供游客休憩．（Ⅰ）若AC=20m，BC=24m，求AB的长度．
（Ⅱ）如图，AB=24m，AD与AB垂直，且∠ADC=120°，∠ABC=θ（45°≤θ≤60°）．记游客通道长度和为L，写出L关于θ的关系式，并求L的最小值．
考点：解三角形的实际应用,在实际问题中建立三角函数模型
专题：应用题,解三角形
分析：（Ⅰ）利用余弦定理，求AB的长度．
（Ⅱ）求出AD，CD，可得出L关于θ的关系式，化简后求L的最小值．
（Ⅱ）求出AD，CD，可得出L关于θ的关系式，化简后求L的最小值．
解答：
解：（Ⅰ）由已知由余弦定理，得AB2=BC2+AC2-2BC•AC•cos60°=242+202-2×24×20×
=496，
∴AB=4
…（4分）
（Ⅱ）在△ACB中，
=
，
∴AC=
=16
sinθ…（5分）
由已知得∠CAB=120°-θ，∠CAD=θ-30°
又∠ADC=120°，∠ACD=90°-θ…（6分）
在△ADC中，
=
=
AD=
=
=16sin2θCD=
=
=16
sin2θ-16sinθcosθ=8
-8
cos2θ-8sin2θ…（9分）
则L=AD+CD=16sin2θ+8
-8
cos2θ-8sin2θ=8
+8sin2θ-8
cos2θ=8
+16sin(2θ-60°)
因45°≤θ≤60°，当θ=45°时，L取到最小值 (8
+8)m …（12分）
| 1 |
| 2 |
∴AB=4
| 31 |
（Ⅱ）在△ACB中，
| AB |
| sin∠ACB |
| AC |
| sin∠ABC |
∴AC=
| 24sinθ |
| sin600 |
| 3 |
由已知得∠CAB=120°-θ，∠CAD=θ-30°
又∠ADC=120°，∠ACD=90°-θ…（6分）
在△ADC中，
| AC |
| sin∠ADC |
| AD |
| sin∠ACD |
| CD |
| sin∠CAD |
| ACsin(900-θ) |
| sin1200 |
16
| ||||
|
| ACsin(θ-300) |
| sin1200 |
16
| ||||||||
|
=16
| 3 |
| 3 |
| 3 |
则L=AD+CD=16sin2θ+8
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
因45°≤θ≤60°，当θ=45°时，L取到最小值 (8
| 3 |
点评：本题考查余弦定理，考查正弦定理，考查三角函数的化简，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
若点M（x，y）为平面区域
上的一个动点，则x+2y的最大值是（ ）
|
| A、-1 | ||
B、-
| ||
| C、0 | ||
| D、1 |
已知函数g（x）是R上的奇函数，且当x＜0时g（x）=-ln（1-x），设函数f（x）=
，若f（2-x2）＞f（x），则实数x的取值范围是（ ）
|
| A、（-∞，1）∪（2，+∞） |
| B、（-∞，-2）∪（1，+∞） |
| C、（1，2） |
| D、（-2，1） |