题目内容
f(n)=1+
+…+
,当n≥2,n∈N*时n+f(1)+f(2)+…+f(n-1)=nf(n),请用数学归纳法给予证明.
| 1 |
| 2 |
| 1 |
| n |
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:数学归纳法的一般步骤是,第一步验证第一项是否成立,第二步假设n=k时候结论成立,去验证n=k+1时候结论是否成立.若都成立即得证.
解答:
证明:1°、当n=2时,等式左边=2+f(1)=2+1=3
等式右边=2f(2)=2(1+
)=3,∴原式成立;…(4分)
2°、假设n=k(k≥2)成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)…(6分)
则当n=k+1时,
等式左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)
=k+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+f(k)+1…(10分)
=(k+1)f(k)+1=(k+1)[f(k)+
=(k+1)f(k+1)
即当n=k+1时,等式也成立.…(12分)
综上1°,2°可得当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n)均成立…(14分)
等式右边=2f(2)=2(1+
| 1 |
| 2 |
2°、假设n=k(k≥2)成立,即k+f(1)+f(2)+…+f(k-1)=kf(k)…(6分)
则当n=k+1时,
等式左边=(k+1)+f(1)+f(2)+…+f(k-1)+f(k)
=k+f(1)+f(2)+…+f(k-1)+f(k)=kf(k)+f(k)+1…(10分)
=(k+1)f(k)+1=(k+1)[f(k)+
| 1 |
| k+1 |
即当n=k+1时,等式也成立.…(12分)
综上1°,2°可得当n≥2,n∈N*时,n+f(1)+f(2)+…+f(n-1)=nf(n)均成立…(14分)
点评:数学归纳法的基本形式:设P(n)是关于自然数n的命题,若1°P(n0)成立(奠基);2°假设P(k)成立(k≥n0),可以推出P(k+1)成立(归纳),则P(n)对一切大于等于n0的自然数n都成立.

练习册系列答案
相关题目
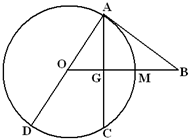 如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12.
如图,已知AD为圆O的直径,直线BA与圆O相切于点A,直线OB与弦AC垂直并相交于点G,与弧AC相交于M,连接DC,AB=10,AC=12. 如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE.
如图,已知BC为⊙O的直径,点A、F在⊙O上,AD⊥BC,垂足为D,BF交AD于E,且AE=BE. 如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.
如图所示,在圆O中,直径AB与弦CD垂直,垂足为E,EF⊥DB,垂足为F,若AB=6,AE=1,求DF•DB的值.