题目内容
如图所示，在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥DB，垂足为F，若AB=6，AE=1，求DF•DB的值．考点：与圆有关的比例线段
专题：直线与圆,立体几何
分析：利用相交弦定理及射影定理求解．
解答：
（本小题12分）
解：在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥DB，垂足为F，
∵AB=6，AE=1，∴BE=5．
∴CE•DE=DE2=AE•BE=5．
在Rt△DEB中，∵EF⊥DB，
∴由射影定理得DF•DB=DE2=5．
（本小题12分） 解：在圆O中，直径AB与弦CD垂直，垂足为E，EF⊥DB，垂足为F，
∵AB=6，AE=1，∴BE=5．
∴CE•DE=DE2=AE•BE=5．
在Rt△DEB中，∵EF⊥DB，
∴由射影定理得DF•DB=DE2=5．
点评：本题考查两条线段长的乘积的求法，是中档题，解题时要认真审题，注意相交弦定理和射影定理的灵活运用．
练习册系列答案
相关题目
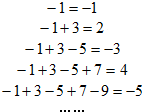观察如图所示5个等式：照图中式子规律：