题目内容
（1）若f′（x0）=6，求
的值；
（2）若函数f（x）=（x2-x-1）e-x，求f（x）的极值．
|
| f(x0-t)-f(x0) |
| 3t |
（2）若函数f（x）=（x2-x-1）e-x，求f（x）的极值．
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：（1）根据导数的定义即可到达结论，
（2）求函数的导数，利用导数和函数极值之间的关系即可得到结论．
（2）求函数的导数，利用导数和函数极值之间的关系即可得到结论．
解答：
解：（1）∵
=
×(-
)=-
f′（x0）=6×(-
)=-2，
（2）∵f（x）=（x2-x-1）e-x，
∴f'（x）=-x（x-3）e-x
由f'（x）＞0，解得0＜x＜3，此时函数单调递增，
由f'（x）＜0，解得x＜0或x＞3，此时函数单调递减，
即当x=0时，f（x）的极小值为-1，
当x=3时，f（x）的极大值为5e-3．
|
| f(x0-t)-f(x0) |
| 3t |
| lim |
| t→0 |
| f(x0-t)-f(x0) |
| -t |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
（2）∵f（x）=（x2-x-1）e-x，
∴f'（x）=-x（x-3）e-x
由f'（x）＞0，解得0＜x＜3，此时函数单调递增，
由f'（x）＜0，解得x＜0或x＞3，此时函数单调递减，
即当x=0时，f（x）的极小值为-1，
当x=3时，f（x）的极大值为5e-3．
点评：本题主要考查导数的定义，以及函数极值的求法，根据导数与极值之间的关系是解决本题的关键．
练习册系列答案
相关题目
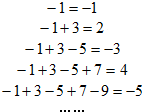观察如图所示5个等式：照图中式子规律：
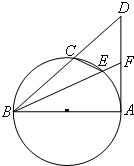如图，BA是圆O的直径，C、E在圆0上，BC、BE的延长线交直线AD于点D、F，BA2=BC•BD．求证：