题目内容
已知等差数列{an}的首项a1及公差d都是整数,且前n项和为Sn,若a1>1,a4>3,S3≤9,则数列{an}的通项公式是 .
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:先由等差数列{an}的首项a1及公差d都是整数,前n项和为Sn,若a1>1,a4>3,S3≤9,设求出数列{an}的首项及公差,进而求出其通项.
解答:
解:∵a1>1,a4>3,S3≤9,
∴a1+3d>3,3a2≤9,
∴d>
,a1+d≤3,
∴a1≤3-d<
.
∵等差数列{an}的首项a1及公差d都是整数
∴a1=2,
<d≤1⇒d=1.
∴an=n+1.
故答案为:an=n+1.
∴a1+3d>3,3a2≤9,
∴d>
| 2 |
| 3 |
∴a1≤3-d<
| 7 |
| 3 |
∵等差数列{an}的首项a1及公差d都是整数
∴a1=2,
| 1 |
| 3 |
∴an=n+1.
故答案为:an=n+1.
点评:解决本题的关键在于利用已知条件求出数列{an}的首项及公差,进而求出其通项.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
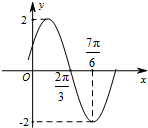 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(x+
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(x+
|
如果执行如图的程序框图,输出的n的值为( )


| A、8 | B、9 | C、.10 | D、11 |
下列四个命题中正确的是( )
| A、两个单位向量一定相等 | ||||||||
| B、两个相等的向量的起点、方向、长度必须都相同 | ||||||||
| C、共线的单位向量必相等 | ||||||||
D、若
|