题目内容
已知f(x)=|x+1|+|x-2|
(Ⅰ)求f(x)>5的解集;
(Ⅱ)若关于x的不等式f(x)<m有解,求实数m的取值范围.
(Ⅰ)求f(x)>5的解集;
(Ⅱ)若关于x的不等式f(x)<m有解,求实数m的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)通过对x取值范围的讨论,去掉绝对值符号,解相应的一次不等式,最后取并集即可求得不等式f(x)>5的解集;
(Ⅱ)利用绝对值不等式的几何意义,可得f(x)min=3,从而可解得实数m的取值范围.
(Ⅱ)利用绝对值不等式的几何意义,可得f(x)min=3,从而可解得实数m的取值范围.
解答:
解:(Ⅰ)∵|x+1|+|x-2|>5,
∴
或
或
,
解得x<-2或x>3,
∴f(x)>5的解集为{x|x<-2或x>3}…5分;
(Ⅱ)∵当x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3,且不等式|x+1|+|x-2|<m有解,
∴m>3,
故实数m的取值范围是(3,+∞)…10分
∴
|
|
|
解得x<-2或x>3,
∴f(x)>5的解集为{x|x<-2或x>3}…5分;
(Ⅱ)∵当x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3,且不等式|x+1|+|x-2|<m有解,
∴m>3,
故实数m的取值范围是(3,+∞)…10分
点评:本题考查绝对值不等式的解法,对x取值范围分类讨论,去掉绝对值符号是解不等式的关键,考查绝对值不等式的几何意义及应用,属于中档题.

练习册系列答案
相关题目
设函数f(x)=
sin(ωx+φ+
)(0<φ<
)的最小正周期为π,且f(-x)=f(x),则( )
| 2 |
| π |
| 4 |
| π |
| 2 |
A、f(x)在(0,
| ||||
B、f(x)在(
| ||||
C、f(x)在(0,
| ||||
D、f(x)在(
|
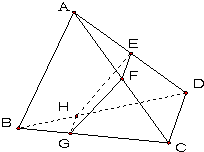 如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,
如图,三棱锥A-BCD被一平面所截,截面为平行四边形EFGH,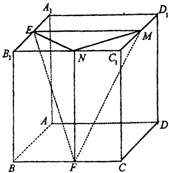 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点. 如图,已知四棱锥P-ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M.
如图,已知四棱锥P-ABCD的底面是矩形,侧面PAB是正三角形,且平面PAB⊥平面ABCD,E是PA的中点,AC与BD的交点为M.