题目内容

已知二阶矩阵A有特征值λ1=3及其对应的一个特征向量
a1
=
1
1
，特征值λ2=-1及其对应的一个特征向量
a2
=
1
-1
，求矩阵A的逆矩阵A-1．
考点：矩阵特征值的定义,变换、矩阵的相等
专题：选作题,矩阵和变换
分析：利用特征值与特征向量的定义，建立方程组，即可求得A，即可求得逆矩阵A-1．
解答： 解：设A=
ab
cd
，则
∵二阶矩阵A有特征值λ1=3及其对应的一个特征向量
a1
=
1
1
，特征值λ2=-1及其对应的一个特征向量
a2
=
1
-1
，
∴
ab
cd
1
1
=3
1
1
，
ab
cd
1
-1
=
1
-1
，
∴
a+b=3
c+d=3
且
a-b=-1
c-d=1
，
∴a=1，b=2，c=2，d=1，
∴A=
12
21
，
∴A-1=
1
3
2
3
2
3
1
3
．
点评：本题主要考查了二阶矩阵，以及特征值与特征向量的计算，考查逆矩阵，正确理解特征值与特征向量是关键，属于中档题．
练习册系列答案
相关题目
下列函数f（x）中，在（0，+∞）上是减函数的是（　　）
A、f（x）=
1
x
-x
B、f（x）=x3
C、f（x）=lnx
D、f（x）=2x
已知{an}是首项a1=2且公比q≠1的等比数列，a1，2a2，3a3依次成等差数列．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）记数列{an}的前n项和为Sn，若不等式
Sn-1
Sn+1-1
＞λ对任意n∈N*恒成立，求实数λ的范围．
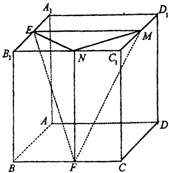如图，正方体ABCD-A1B1C1D1的棱长为1，E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点．
（Ⅰ）用向量方法求直线EF与MN的夹角；
（Ⅱ）求二面角N-EF-M的平面角的正切值．
已知sinθ，cosθ是关于x的方程x2-ax+a=0（a∈R）的两个根．
（1）求cos3（
π
2
-θ）+sin3（
π
2
-θ）的值；
（2）求tan（π-θ）-
1
tanθ
的值．
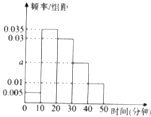经统计，某校学生上学路程所需要时间全部介于0与50之间（单位：分钟），现从在校学生中随机抽取100人，按上学所需时间分组如下：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到如图所示的频率分布直方图．
（Ⅰ）根据图中数据求a的值；
（Ⅱ）若从第3，4，5组中用分层柚样的方法抽取6人参与交通安全问卷调查，应从这三组中各抽取几人？
（Ⅲ）在（Ⅱ）的条件下，若从这6人中随机抽取2人参加交通安全宣传活动，求第4组至少有1人被抽中的概率．
（理）已知函数f（x）对任意x∈R都有f（x）+f（1-x）=2．
（1）求f（
1
2
）和f（
1
n
）+f（
n-1
n
）（n∈N*）的值；
（2）数列f（x）满足an=f（0）+f（
1
n
）+f（
2
n
）+…+f（
n-1
n
）+f（1），（n∈N*）求证：数列{an}是等差数列；
（3）bn=
1
an-1
，Sn=
4n
2n+1
，Tn=b12+b22+b32+…+bn2，试比较Tn与Sn的大小．
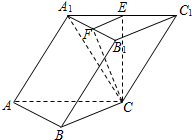在斜三棱柱ABC-A1B1C1中，已知侧面ACC1A1⊥底面ABC，A1C=C1C，E，F分别是A1C1、A1B1的中点．
（1）求证：EF∥平面BB1C1C；
（2）求证：平面ECF⊥平面ABC．
数列{an}中，a1=8，a4=2，且满足an+2-2an+1+an=0（n∈N*）．
（1）求数列的通项公式an；
（2）求和：a2+a5+a8+…+a92；
（3）求
n
k=1
|ak|的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网