题目内容

某企业要建造一个容积为18m3，深为2m的长方体形无盖贮水池，如果池底和池壁每平方米的造价分别为200元和150元，怎样设计该水池可使得能总造价最低？最低总造价为多少？
考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：设底面的长与宽分别为xm，ym，水池总造价为z元，建立函数关系式，求出z的最小值．
解答： 解：设底面的长为xm，宽为ym，水池总造价为z元，
则由容积为18m3，可得：2xy=18，因此xy=9，
z=200×9+150（2×2x+2×2y）=1800+600（x+y）≥1800+600•2
xy
=5400
当且仅当x=y=3时，取等号．
所以，将水池的地面设计成边长为3m的正方形时总造价最低，最低总造价为5400元．
点评：此题首先需要由实际问题向数学问题转化，即建立函数关系式，然后求函数的最值，其中用到了均值不等式定理．
练习册系列答案
相关题目
设数列{an}的前n项和Sn=n2+2n（n∈N*）．
（1）写出数列的前三项a1，a2，a3；
（2）求通项an．
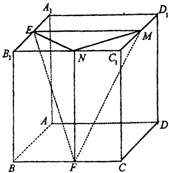如图，正方体ABCD-A1B1C1D1的棱长为1，E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点．
（Ⅰ）用向量方法求直线EF与MN的夹角；
（Ⅱ）求二面角N-EF-M的平面角的正切值．
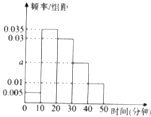经统计，某校学生上学路程所需要时间全部介于0与50之间（单位：分钟），现从在校学生中随机抽取100人，按上学所需时间分组如下：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到如图所示的频率分布直方图．
（Ⅰ）根据图中数据求a的值；
（Ⅱ）若从第3，4，5组中用分层柚样的方法抽取6人参与交通安全问卷调查，应从这三组中各抽取几人？
（Ⅲ）在（Ⅱ）的条件下，若从这6人中随机抽取2人参加交通安全宣传活动，求第4组至少有1人被抽中的概率．
（理）已知函数f（x）对任意x∈R都有f（x）+f（1-x）=2．
（1）求f（
1
2
）和f（
1
n
）+f（
n-1
n
）（n∈N*）的值；
（2）数列f（x）满足an=f（0）+f（
1
n
）+f（
2
n
）+…+f（
n-1
n
）+f（1），（n∈N*）求证：数列{an}是等差数列；
（3）bn=
1
an-1
，Sn=
4n
2n+1
，Tn=b12+b22+b32+…+bn2，试比较Tn与Sn的大小．
解下列不等式：
（1）-3x2+5x-4＜0
（2）x（1-x）＞x（2x-3）+1．
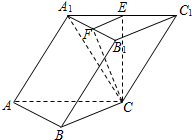在斜三棱柱ABC-A1B1C1中，已知侧面ACC1A1⊥底面ABC，A1C=C1C，E，F分别是A1C1、A1B1的中点．
（1）求证：EF∥平面BB1C1C；
（2）求证：平面ECF⊥平面ABC．
用分析法证明：若a＞b＞0，m＞0，则
a
b
＞
a+m
b+m
．
某公司近年来科研费用支出x万元与公司所获得利润y万元之间有如下的统计数据：
x2345
Y18273235
（Ⅰ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
y
=
b
x+
a
；
（Ⅱ）试根据（2）求出的线性回归方程，预测该公司科研费用支出为10万元时公司所获得的利润．
参考公式：若变量x和y用最小二乘法求出y关于x的线性回归方程为：
y
=
b
x+
a
，其中：
b
=
n
i=1
xiyi-n
.
x
.
y
n
i=1
xi2-n(
.
x
)2
，
a
=
.
y
-
b
.
x
，参考数值：2×18+3×27+4×32+5×35=420．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网