题目内容
某园林局对1000株树木的生长情况进行调查,其中杉树600株,槐树400株.现用分层抽样方法从这1000株树木中随机抽取100株,杉树与槐树的树干周长(单位:cm)的抽查结果如下表:
(1)求x,y值及估计槐树树干周长的众数;
(2)如果杉树的树干周长超过60cm就可以砍伐,请估计该片园林可以砍伐的杉树有多少株?
(3)树干周长在30cm到40cm之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 杉树 | 6 | 19 | 21 | x |
| 槐树 | 4 | 20 | y | 6 |
(2)如果杉树的树干周长超过60cm就可以砍伐,请估计该片园林可以砍伐的杉树有多少株?
(3)树干周长在30cm到40cm之间的4株槐树有1株患虫害,现要对这4株树逐一进行排查直至找出患虫害的树木为止.求排查的树木恰好为2株的概率.
考点:古典概型及其概率计算公式,众数、中位数、平均数
专题:概率与统计
分析:(1)首先求出样本中槐树和杉树的株数,继而求出x,y的值,根据的众数的定义可以轻松求出.
(2)根据用样本来估计总体的方法求得需要砍杀的杉树的株数.
(3)一一列举求取满足条件的基本事件,找到满足有虫的那株的基本事件,根据概率公式计算即可.
(2)根据用样本来估计总体的方法求得需要砍杀的杉树的株数.
(3)一一列举求取满足条件的基本事件,找到满足有虫的那株的基本事件,根据概率公式计算即可.
解答:
解 (1)按分层抽样方法随机抽取100株,可得槐树为40株,杉树为60株,
∴x=60-6-19-21=14,y=40-4-20-6=10.
估计槐树树干周长的众数为45cm.
(2)
×600=140,
估计该片园林可以砍伐的杉树有140株.
(3)设4株树为B1,B2,B3,D,设D为有虫害的那株,
基本事件为(D),(B1,D),(B2,D),(B3,D),(B1,B2,D),(B1,B3,D),(B2,B1,D),(B2,B3,D),(B3,B1,D),(B3,B2,D),
(B1,B2,B3),(B1,B3,B2),(B2,B1,B3),(B2,B3,B1),(B3,B1,B2),(B3,B2,B1)共16种,
设事件A:排查的树木恰好为2株,事件A包含(B1,D),(B2,D),(B3,D)3种,
∴P(A)=
.
∴x=60-6-19-21=14,y=40-4-20-6=10.
估计槐树树干周长的众数为45cm.
(2)
| 14 |
| 60 |
估计该片园林可以砍伐的杉树有140株.
(3)设4株树为B1,B2,B3,D,设D为有虫害的那株,
基本事件为(D),(B1,D),(B2,D),(B3,D),(B1,B2,D),(B1,B3,D),(B2,B1,D),(B2,B3,D),(B3,B1,D),(B3,B2,D),
(B1,B2,B3),(B1,B3,B2),(B2,B1,B3),(B2,B3,B1),(B3,B1,B2),(B3,B2,B1)共16种,
设事件A:排查的树木恰好为2株,事件A包含(B1,D),(B2,D),(B3,D)3种,
∴P(A)=
| 3 |
| 16 |
点评:本题主要考查了分成抽样、众数、古典概型的概率的求法,属于基础题.

练习册系列答案
相关题目
函数y=loga(3x-2)(a>0,a≠1)的图过定点A,则A点坐标是( )
A、(0,
| ||
B、(
| ||
| C、(1,0) | ||
| D、(0,1) |
 如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,
如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,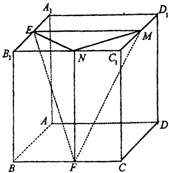 如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.
如图,正方体ABCD-A1B1C1D1的棱长为1,E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点.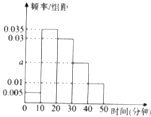 经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.
经统计,某校学生上学路程所需要时间全部介于0与50之间(单位:分钟),现从在校学生中随机抽取100人,按上学所需时间分组如下:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到如图所示的频率分布直方图.