题目内容
已知
，
满足：|
|=3，|
|=4，|
-
|=5，则|
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | ||
B、
| ||
| C、5 | ||
| D、4 |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意，求出2
•
的值，即可求出|
+
|的值．
| a |
| b |
| a |
| b |
解答：
解：根据题意，得；
(
-
)2=
2-2
•
+
2
=32-2
•
+42=52，
∴2
•
=0；
∴|
+
|=
=
=
=5．
故答案为：C．
(
| a |
| b |
| a |
| a |
| b |
| b |
=32-2
| a |
| b |
∴2
| a |
| b |
∴|
| a |
| b |
(
|
=
|
=
| 32+0+42 |
=5．
故答案为：C．
点评：本题考查了利用平面向量的数量积求向量的模长的问题，解题时应按照平面向量的运算法则进行计算即可，是基础题．
练习册系列答案
相关题目
如图已知空间四面体D一ABC的每条边都等于1，点E，F分别是AB，AD的中点，则设O为△ABC的外心，且
+
+
=
，|
|=1则
•（
+
）值是（ ）
| OA |
| OB |
| 3 |
| OC |
| 0 |
| AB |
| CO |
| CA |
| CB |
A、2-
| ||
| B、2 | ||
C、2+
| ||
| D、4 |
已知|
|=4|
|≠0，且关于x的方程2x2+|
|x+
•
=0有实根，则
与
的夹角的取值范围是（ ）
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、[0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知向量
=（cos
，sin
），
=（-1，0）．则向量
与
的夹角为（ ）
| a |
| π |
| 6 |
| π |
| 6 |
| b |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、
|
如图，在正方体ABCD-A1B1C1D1中，M，N分别是BC1，CD1的中点，则下列说法错误的是（ ）
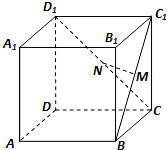
| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
设曲线C：x2=y上有两个动点A、B，直线AB与曲线C在A点处切线垂直，则点B到y轴距离的最小值是（ ）
A、2
| ||
B、
| ||
C、
| ||
| D、2 |
已知log
x1=logax2=log（a+1）x3＞0，0＜a＜1，则x1，x2，x3的大小关系是（ ）
| a |
| A、x3＜x2＜x1 |
| B、x2＜x1＜x3 |
| C、x1＜x3＜x2 |
| D、x2＜x3＜x1 |