题目内容
若函数f(x)=
-
+ln3的导函数为f′(x),则f′(x)=( )
| x |
| 1 |
| x |
A、f′(x)=
| ||||||||
B、f′(x)=
| ||||||||
C、f′(x)=
| ||||||||
D、f′(x)=
|
考点:导数的运算
专题:导数的概念及应用
分析:根据导数的运算法则求导即可.
解答:
解:f′(x)=
x-
+
=
+
.
故选:D.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x2 |
| 1 | ||
2
|
| 1 |
| x2 |
故选:D.
点评:本题主要考查了导数的运算法则,关键是掌握基本的导数公式.

练习册系列答案
相关题目
已知a=log23,b=log0.53,c=4-
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| A、a>c>b |
| B、a<c<b |
| C、a<b<c |
| D、a>b>c |
已知|
|=4|
|≠0,且关于x的方程2x2+|
|x+
•
=0有实根,则
与
的夹角的取值范围是( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
等差数列{an}中,a6+a7+a8=75,则a3+a11=( )
| A、48 | B、49 | C、50 | D、51 |
如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
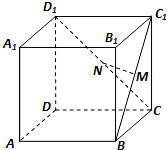

| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
向量
=(2,x),
=(-1,2),若
与
-2
垂直,则x等于( )
| a |
| b |
| b |
| a |
| b |
| A、2 | B、-4 | C、-6 | D、6 |
设椭圆
+
=1的两焦点为F1、F2,P是椭圆上一点,且∠F1PF2=90°,则△F1P F2的面积为( )
| x2 |
| 9 |
| y2 |
| 25 |
| A、18 | B、15 | C、9 | D、5 |
已知集合A={x|x=2n-l,n∈Z},B={x|x2一4x<0},则A∩B=( )
| A、{1} |
| B、{x|1<x<4} |
| C、{1,3} |
| D、{1,2,3,4} |
 如图(1),在△ABC中,AB⊥AC,AD⊥BC,D是垂足,则AB2=BD•BC,该结论称为射影定理.如图(2),在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,可以得到结论:
如图(1),在△ABC中,AB⊥AC,AD⊥BC,D是垂足,则AB2=BD•BC,该结论称为射影定理.如图(2),在三棱锥A-BCD中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,类比射影定理,可以得到结论: