题目内容
下列命题中正确命题的个数是( )
①对任意两向量
、
,均有:|
|-|
|<|
|+|
|
②若单位向量
、
夹角为120°,则当|2
+x
|(x∈R)取最小值时,x=1
③若
=(6,-3),
=(3,-4),
=(5-m,-3-m),∠ABC为锐角,则实数m的取值范围是m>-
④在四边形ABCD中,(
+
)-(
+
)=
.
①对任意两向量
| a |
| b |
| a |
| b |
| a |
| b |
②若单位向量
| a |
| b |
| a |
| b |
③若
| OB |
| OA |
| OC |
| 3 |
| 4 |
④在四边形ABCD中,(
| AB |
| BC |
| CD |
| DA |
| 0 |
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:①让|
|=0,便不符合该命题,所以该命题错误.
②为求|2
+x
|,先求(2
+x
)2,只要让(2
+x
)2最小即可.
③由∠ABC为锐角,能得到0<cos∠ABC<1,根据向量的夹角计算公式便可得到m的取值范围.
④根据向量的加法,减法运算便可判断该命题.
| b |
②为求|2
| a |
| b |
| a |
| b |
| a |
| b |
③由∠ABC为锐角,能得到0<cos∠ABC<1,根据向量的夹角计算公式便可得到m的取值范围.
④根据向量的加法,减法运算便可判断该命题.
解答:
解:①若设|
|=0,则有|
|-|
|=|
|+|
|.
②(2
+x
)2=4+4x×(-
)+x2=x2-2x+4=(x-1)2+3≥3
∴x=1时,|2
+x
|取得最小值.所以该命题正确.
③根据已知条件:
=(-3,-1),
=(-m-1,-m);
∴
•
=4m+3,|
|=
,|
|=2m2+2m+1;
∴cos∠ABC=
;
∵∠ABC为锐角,∴0<
<1,解得m>
, 或m<
,所以该命题错误.
④(
+
)-(
+
)=2
,所以本命题错误.
所以正确的命题个数为:1.
故选B.
| b |
| a |
| b |
| a |
| b |
②(2
| a |
| b |
| 1 |
| 2 |
∴x=1时,|2
| a |
| b |
③根据已知条件:
| BA |
| BC |
∴
| BA |
| BC |
| BA |
| 10 |
| BC |
∴cos∠ABC=
| 4m+3 |
| 2m2+2m+1 |
∵∠ABC为锐角,∴0<
| 4m+3 |
| 2m2+2m+1 |
1+
| ||
| 2 |
1-
| ||
| 2 |
④(
| AB |
| BC |
| CD |
| DA |
| AC |
所以正确的命题个数为:1.
故选B.
点评:考查的知识点有:向量的数量积的运算公式,向量夹角的计算公式,向量的加减法,两向量模的差与模的和的大小关系,注意求一个向量的长度,先求该向量的平方的方法.

练习册系列答案
相关题目
如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
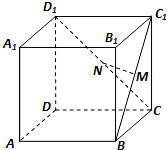

| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
设f:A→是从A到B的一个映射,其中A=B={(x,y)|x,y∈R}.f:(x,y)→(x+y,x-y),则A中的元素(1,2)在B中的象是( )
| A、(3,-1) | ||||
B、(
| ||||
| C、(-1,3) | ||||
D、(-
|
已知log
x1=logax2=log(a+1)x3>0,0<a<1,则x1,x2,x3的大小关系是( )
| a |
| A、x3<x2<x1 |
| B、x2<x1<x3 |
| C、x1<x3<x2 |
| D、x2<x3<x1 |
已知集合A={x|x=2n-l,n∈Z},B={x|x2一4x<0},则A∩B=( )
| A、{1} |
| B、{x|1<x<4} |
| C、{1,3} |
| D、{1,2,3,4} |
设直线ax+by+c=0的倾斜角为θ(θ≠0,θ≠
),且sinθ-cosθ=0,则a、b满足( )
| π |
| 2 |
| A、a+b=1 |
| B、a-b=1 |
| C、a+b=0 |
| D、a-b=0 |
将函数y=sin3x的图象作下列平移可得y=sin(3x+
)的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
若复数(a2-3a+2)+(a-2)i是纯虚数,则实数a的值为( )
| A、1 | B、2 | C、1或2 | D、-1 |