题目内容
极坐标方程ρ=sin(θ+3)(θ为参数)表示的曲线是( )
| A、双曲线 | B、椭圆 | C、抛物线 | D、圆 |
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:极坐标方程ρ=sin(θ+3)(θ为参数)化为ρ2=ρsinθcos3+ρcosθsin3,再利用x=ρcosθ,y=ρsinθ即可化为直角坐标方程,进而判断出.
解答:
解:极坐标方程ρ=sin(θ+3)(θ为参数)化为ρ2=ρsinθcos3+ρcosθsin3,
∴x2+y2=ycos3+xsin3,
配方为(x-
sin3)2+(y-
cos3)2=
.
∴此方程表示的是以(
sin3,
cos3)为圆心,
为半径的圆.
故选:D.
∴x2+y2=ycos3+xsin3,
配方为(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴此方程表示的是以(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查了圆的极坐标方程化为直角坐标方程的方法,属于基础题.

练习册系列答案
相关题目
已知|
|=4|
|≠0,且关于x的方程2x2+|
|x+
•
=0有实根,则
与
的夹角的取值范围是( )
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
如图,在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
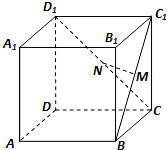

| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
向量
=(2,x),
=(-1,2),若
与
-2
垂直,则x等于( )
| a |
| b |
| b |
| a |
| b |
| A、2 | B、-4 | C、-6 | D、6 |
设曲线C:x2=y上有两个动点A、B,直线AB与曲线C在A点处切线垂直,则点B到y轴距离的最小值是( )
A、2
| ||
B、
| ||
C、
| ||
| D、2 |
设椭圆
+
=1的两焦点为F1、F2,P是椭圆上一点,且∠F1PF2=90°,则△F1P F2的面积为( )
| x2 |
| 9 |
| y2 |
| 25 |
| A、18 | B、15 | C、9 | D、5 |
设f:A→是从A到B的一个映射,其中A=B={(x,y)|x,y∈R}.f:(x,y)→(x+y,x-y),则A中的元素(1,2)在B中的象是( )
| A、(3,-1) | ||||
B、(
| ||||
| C、(-1,3) | ||||
D、(-
|
将函数y=sin3x的图象作下列平移可得y=sin(3x+
)的图象( )
| π |
| 6 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|