题目内容
已知函数f（x）=aln（x+
）+bsinx+1满足f（2）=3，则f（-2）等于（ ）
| x2+1 |
| A、-3 | B、-1 | C、0 | D、1 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：函数f（x）是非奇非偶函数，但由函数奇偶性的性质可知：f（x）-1=aln（x+
）+bsinx为奇函数，故可构造此函数进行求解．
| x2+1 |
解答：
解：令g（x）=f（x）-1=aln（x+
）+bsinx，
∵g（-x）=aln（-x+
）-bsinx=-[aln（x+
）+bsinx]=-g（x），
由函数奇偶性的性质可知g（x）为奇函数，
∵f（2）=3，
∴g（2）=f（2）-1=2，
∴g（-2）=-2，
∴f（-2）=g（-2）+1=-1
故选：B
| x2+1 |
∵g（-x）=aln（-x+
| x2+1 |
| x2+1 |
由函数奇偶性的性质可知g（x）为奇函数，
∵f（2）=3，
∴g（2）=f（2）-1=2，
∴g（-2）=-2，
∴f（-2）=g（-2）+1=-1
故选：B
点评：本题考查的知识点是函数奇偶性的性质，其中构造函数g（x）=f（x）-1=aln（x+
）+bsinx，是解答的关键．
| x2+1 |
练习册系列答案
阅读快车系列答案
相关题目
如图已知空间四面体D一ABC的每条边都等于1，点E，F分别是AB，AD的中点，则如图，在正方体ABCD-A1B1C1D1中，M，N分别是BC1，CD1的中点，则下列说法错误的是（ ）
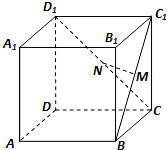
| A、MN与AB1平行 |
| B、MN与CC1垂直 |
| C、MN与AC垂直 |
| D、MN与BD平行 |
设曲线C：x2=y上有两个动点A、B，直线AB与曲线C在A点处切线垂直，则点B到y轴距离的最小值是（ ）
A、2
| ||
B、
| ||
C、
| ||
| D、2 |
设椭圆
+
=1的两焦点为F1、F2，P是椭圆上一点，且∠F1PF2=90°，则△F1P F2的面积为（ ）
| x2 |
| 9 |
| y2 |
| 25 |
| A、18 | B、15 | C、9 | D、5 |
在一次物理实验课上，某同学在弹性限度范围内，将弹簧劲度系数为60N/m的一弹簧从平衡位置拉到离开平衡位置的
m处，则该同学克服弹力所做的功为（ ）
| 1 |
| 4 |
| A、15 | ||
B、
| ||
C、
| ||
D、
|
设f：A→是从A到B的一个映射，其中A=B={（x，y）|x，y∈R}．f：（x，y）→（x+y，x-y），则A中的元素（1，2）在B中的象是（ ）
| A、（3，-1） | ||||
B、（
| ||||
| C、（-1，3） | ||||
D、（-
|
已知log
x1=logax2=log（a+1）x3＞0，0＜a＜1，则x1，x2，x3的大小关系是（ ）
| a |
| A、x3＜x2＜x1 |
| B、x2＜x1＜x3 |
| C、x1＜x3＜x2 |
| D、x2＜x3＜x1 |
若复数（a2-3a+2）+（a-2）i是纯虚数，则实数a的值为（ ）
| A、1 | B、2 | C、1或2 | D、-1 |