Question

第十七届亚运会于2014年9月19日至10月4日在韩国仁川举行．为了搞好接待工作，组委会在首尔大学某学院招募了12名男志愿者和18名女志愿者从事礼宾接待和语言翻译工作，将这30名志愿者的身高（单位：cm）编成茎叶图（如图所示）：

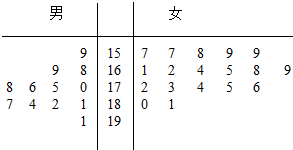
组委会安排决定：身高175cm以上（包含175cm）的志愿者从事礼宾接待，身高在175cm以下的志愿者从事语言翻译．
（Ⅰ）如果从分层抽样的方法从从事礼宾接待的志愿者和从事语言翻译的志愿者中抽取5人，再从这5人中随机选2人，那么至少有一人是从事礼宾接待的志愿者的概率是多少？
（Ⅱ）若从所有从事礼宾接待的志愿者中随机选3名志愿者，用ξ表示从事礼宾接待的志愿者中女志愿者的人数，试写出ξ的分布列，并求出ξ的数学期望．

Answer 1

考点：离散型随机变量及其分布列,茎叶图,古典概型及其概率计算公式,离散型随机变量的期望与方差

专题：概率与统计

分析：（I）先用分层抽样的方法，计算出每个人被抽中的概率，再利用对立事件的概率和为1可求得结果；（II）由题意分别计算出ξ取值为0，1，2，3时各自的概率，然后列出分布列并求出期望．

解答： 解：（I）根据茎叶图，有从事礼宾接待的志愿者12人，有从事语言翻译的志愿者18人，用分层抽样的方法，每个人被抽中的概率是

5

30

=

1

6

．
所以抽中的从事礼宾接待的志愿者有12×

1

6

=2人，从事语言翻译的志愿者有18×

1

6

=3人．
用事件A表示“至少有1名从事礼宾接待的志愿者被选中”，则它的对立事件

.

A

表示“没有1名从事礼宾接待的志愿者被选中”，
则P(A)=1-P(

.

A

)=1-

C 2 3

C 2 5

=

7

10

（II）由题意：ξ的可能取值为0，1，2，3．
则P(ξ=0)=

C 3 8

C 3 12

=

14

55

，P(ξ=1)=

C 1 4 C 2 8

C 3 12

=

28

55

，P(ξ=2)=

C 2 4 C 1 8

C 3 12

=

12

55

，P(ξ=3)=

C 3 4

C 3 12

=

1

55

，
因此，

ξ	0	1	2	3
p	14 55	28 55	12 55	1 55

故Eξ=0×

14

55

+1×

28

55

+2×

12

55

+3×

1

55

=1

点评：本题考查知识点茎叶图；对立事件的概率；离散型随机变量的分布列及期望，基本知识的应用．