题目内容
设函数f(x)=
-ax2,其中a∈R,
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有2个不同的零点,求a的取值范围.
| |x| |
| x+2 |
(1)当a=2时,求函数f(x)的零点;
(2)当a>0时,求证:函数f(x)在(0,+∞)内有且仅有一个零点;
(3)若函数f(x)有2个不同的零点,求a的取值范围.
考点:函数的零点
专题:函数的性质及应用
分析:(1)当a=2时,求出函数的表达式,令|x|-2x2(x+2)=0,可得不等式组,然后解不等式组,求出函数f(x)的零点即可;
(2)当a>0,x>0时,令f(x)=0,可得x(1-ax2-2ax)=0,解方程,求出函数f(x)在(0,+∞)内的零点即可;
(3)函数f(x)有2个不同的零点,①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;②当x≠0时,可得y=
与y=a(x+2)的图象在平面直角坐标系中有2个不同的交点,分别画出它们的图象,判断出a的取值范围即可.
(2)当a>0,x>0时,令f(x)=0,可得x(1-ax2-2ax)=0,解方程,求出函数f(x)在(0,+∞)内的零点即可;
(3)函数f(x)有2个不同的零点,①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;②当x≠0时,可得y=
| |x| |
| x2 |
解答:
 解:(1)当a=2时,函数f(x)=
解:(1)当a=2时,函数f(x)=
,
令|x|-2x2(x+2)=0,
可得
①或
②,
由①可得 x=0,x=
+1,或x=
-1;
由②可得x=
-1,
综上,当a=2时,函数f(x)的零点为x=0,x=
+1,x=
-1或x=
-1;
(2)当a>0,x>0时,
函数f(x)=
,
令f(x)=0,
可得x(1-ax2-2ax)=0,
解得x=-1+
,x=0(舍去),或x=-1-
(舍去),
即函数f(x)在(0,+∞)内有且仅有一个零点x=-1+
;
(3)函数f(x)有2个不同的零点,
①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;
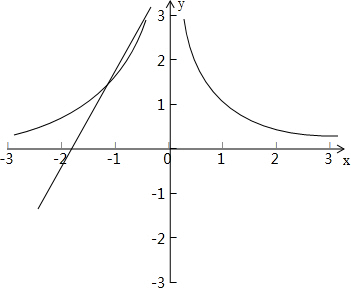
②当x≠0时,可得y=
与y=a(x+2)的图象在平面直角坐标系中有3个不同的交点,
分别画出它们的图象如下:
所以若函数f(x)有2个不同的零点,
求a的取值范围为(-∞,0).
 解:(1)当a=2时,函数f(x)=
解:(1)当a=2时,函数f(x)=| |x|-2x2(x+2) |
| x+2 |
令|x|-2x2(x+2)=0,
可得
|
|
由①可得 x=0,x=
| ||
| 2 |
| ||
| 2 |
由②可得x=
| ||
| 2 |
综上,当a=2时,函数f(x)的零点为x=0,x=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)当a>0,x>0时,
函数f(x)=
| x-ax3-2ax2 |
| x+2 |
令f(x)=0,
可得x(1-ax2-2ax)=0,
解得x=-1+
| 2 |
| 2 |
即函数f(x)在(0,+∞)内有且仅有一个零点x=-1+
| 2 |
(3)函数f(x)有2个不同的零点,
①x=0时,f(0)=0,所以x=0是函数f(x)的一个零点;
②当x≠0时,可得y=
| |x| |
| x2 |
分别画出它们的图象如下:
所以若函数f(x)有2个不同的零点,
求a的取值范围为(-∞,0).
点评:题主要考查了函数的零点与方程的根的关系,考查了分类讨论的数学思想,属于中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
已知半径是13的球面上有A、B、C三点,AB=6,BC=8,AC=10,则球心到截面ABC的距离为( )
| A、12 | B、8 | C、6 | D、5 |
某产品的广告费用x万元与销售额y万元的统计数据如下表:
根据上表可得回归方程
=bx+a中b为9.4,据此模型预报广告费用为6万元时,销售额为65.5,则a,m为( )
| 广告费用x(万元) | 4 | 2 | 3 | 5 |
| 销售额y(万元) | 49 | 26 | 39 | m |
 |
| y |
| A、a=9.1,m=54 |
| B、a=9.1,m=53 |
| C、a=9.4,m=52 |
| D、a=9.2,m=54 |
已知函数f(x)=x2+(m-2)x+m2+12为偶函数,则m的值是( )
| A、1 | B、2 | C、3 | D、4 |