题目内容
18.已知数列{an}的前n项和为Sn,且满足an+Sn=2n+1.(1)求证:数列{an-2}为等比数列;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn.
分析 (1)利用递推关系可得:2an-an-1=2,变形为:an-2=$\frac{1}{2}({a}_{n-1}-2)$,即可证明.
(2)利用等比数列的通项公式即可得出;
(3)利用等比数列的前n项和公式即可得出.
解答 (1)证明:∵an+Sn=2n+1,∴当n=1时,2a1=3,解得a1=$\frac{3}{2}$.
当n≥2时,an-1+Sn-1=2(n-1)+1,
∴2an-an-1=2,
变形为:an-2=$\frac{1}{2}({a}_{n-1}-2)$,
∴数列{an-2}为等比数列,首项为-$\frac{1}{2}$,公比为$\frac{1}{2}$.
(2)解:由(1)可得:an-2=$-\frac{1}{2}×(\frac{1}{2})^{n-1}$=-$(\frac{1}{2})^{n}$,
∴an=2-$(\frac{1}{2})^{n}$,
(3)解:数列{an}的前n项和Sn=2n-$\frac{\frac{1}{2}[1-(\frac{1}{2})^{n}]}{1-\frac{1}{2}}$
=2n-1+$(\frac{1}{2})^{n}$.
点评 本题考查了等比数列的通项公式与前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\\{y≤a(x-4)}\end{array}\right.$,若z=x+2y的最大值为2,则a=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
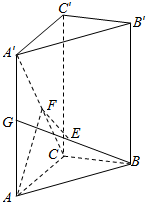 已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.
已知直三棱柱ABC-A′B′C′中,∠ACB=90°,BE=GE,AG=A′G,F是线段A′C上的点,EF∥平面ACB.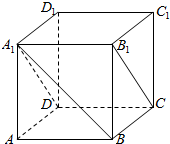 (1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.
(1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.