题目内容
7.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\\{y≤a(x-4)}\end{array}\right.$,若z=x+2y的最大值为2,则a=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义即可得到结论.
解答  解:先作出不等式$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\end{array}\right.$对应的区域,
解:先作出不等式$\left\{\begin{array}{l}{x≥1}\\{x-y≤3}\end{array}\right.$对应的区域,
若z=x+2y的最大值为2,则x+2y=2,
直线y=a(x-4)过定点(4,0),
则直线x+2y=2与x-y=3相交于A,
由$\left\{\begin{array}{l}{x+2y=2}\\{x-y=3}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=-\frac{1}{3}}\end{array}\right.$,即A($\frac{8}{3}$,-$\frac{1}{3}$),
同时A也在直线y=a(x-4)上,
即a($\frac{8}{3}$-4)=-$\frac{1}{3}$,
即-$\frac{4}{3}$a=-$\frac{1}{3}$,得a=$\frac{1}{4}$,
故选:A.
点评 本题主要考查线性规划的应用,根据目标函数的最大值,作出目标函数,求出目标函数和条件对应直线的交点坐标是解决本题的关键.

练习册系列答案
相关题目
2.P={x|2x2-7x+5<0},Q={x|0<x<10},那么( )
| A. | P∩Q=∅ | B. | P⊆Q | C. | Q⊆P | D. | P∪Q=R |
8.已知函数f(ex)=x,则f(2)=( )
| A. | 2 | B. | e2 | C. | log2e | D. | ln2 |
5.下列结论中,正确的是( )
| A. | 三角形绕其一边旋转一周后成一个圆锥 | |
| B. | 一个直角梯形绕其一边旋转一周后成为一个圆台 | |
| C. | 平行四边形绕其一边旋转一周后成为圆柱 | |
| D. | 圆面绕其一条直径旋转一周后成为一个球 |
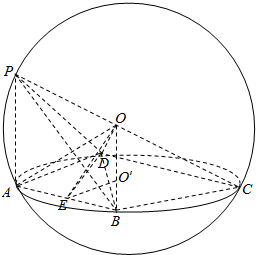 已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,∠BCD=90°
已知点P,A,B,C,D是球O表面上的点,且球心O在线段PC上,PA⊥平面ABCD,E为AB的中点,∠BCD=90° 如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,BC=2AB=4,$A{A_1}=2\sqrt{2}$,E是A1D1的中点.