题目内容
已知椭圆:
+
=1(a>b>0),离心率为
,焦点F1(0,-c),F2(0,c)过F1的直线交椭圆于M,N两点,且△F2MN的周长为4.
(Ⅰ)求椭圆方程;
(Ⅱ) 直线l与y轴交于点P(0,m)(m≠0),与椭圆C交于相异两点A,B且
=λ
.若
+λ
=4
,求m的取值范围.
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆方程;
(Ⅱ) 直线l与y轴交于点P(0,m)(m≠0),与椭圆C交于相异两点A,B且
| AP |
| PB |
| OA |
| OB |
| OP |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)先离心率为
,△F2MN的周长为4,可求出a,b,c的值,从而得到答案.
(2)先设l与椭圆C交点为A、B的坐标,然后联立直线和椭圆方程消去y,得到关于x的一元二次方程,进而得到两根之和、两根之积,根据
=λ
,
+λ
=4
,可得λ=3,再利用韦达定理,即可解出m的范围.
| ||
| 2 |
(2)先设l与椭圆C交点为A、B的坐标,然后联立直线和椭圆方程消去y,得到关于x的一元二次方程,进而得到两根之和、两根之积,根据
| AP |
| PB |
| OA |
| OB |
| OP |
解答:
解:(Ⅰ)由题意,4a=4,
=
,
∴a=1,c=
,
∴b=
=
,
∴椭圆方程方程为y2+
=1;
(Ⅱ)设l与椭圆C交点为A(x1,y1),B(x2,y2)
由
得(k2+2)x2+2kmx+(m2-1)=0
△=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0(*)
∴x1+x2=-
,x1x2=
,
∵
=λ
,
+λ
=4
,
∴λ=3
∴-x1=3x2
∴x1+x2=-2x2,x1x2=-3x22,
∴3(x1+x2)2+4x1x2=0,
∴3(-
)2+4•
=0,
整理得4k2m2+2m2-k2-2=0
m2=
时,上式不成立;m2≠
时,k2=
,
由(*)式得k2>2m2-2
∵k≠0,
∴k2=
>0,
∴-1<m<-
或
<m<1
即所求m的取值范围为(-1,-
)∪(
,1).
| c |
| a |
| ||
| 2 |
∴a=1,c=
| ||
| 2 |
∴b=
| a2-c2 |
| ||
| 2 |
∴椭圆方程方程为y2+
| x2 | ||
|
(Ⅱ)设l与椭圆C交点为A(x1,y1),B(x2,y2)
由
|
△=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0(*)
∴x1+x2=-
| 2km |
| k2+2 |
| m2-1 |
| k2+2 |
∵
| AP |
| PB |
| OA |
| OB |
| OP |
∴λ=3
∴-x1=3x2
∴x1+x2=-2x2,x1x2=-3x22,
∴3(x1+x2)2+4x1x2=0,
∴3(-
| 2km |
| k2+2 |
| m2-1 |
| k2+2 |
整理得4k2m2+2m2-k2-2=0
m2=
| 1 |
| 4 |
| 1 |
| 4 |
| 2-2m2 |
| 4m2-1 |
由(*)式得k2>2m2-2
∵k≠0,
∴k2=
| 2-2m2 |
| 4m2-1 |
∴-1<m<-
| 1 |
| 2 |
| 1 |
| 2 |
即所求m的取值范围为(-1,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查椭圆的标准方程、基本性质和直线与椭圆的综合问题.直线和圆锥曲线的综合题是高考的重点题目,要强化学习.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证:
如图,PA,PB是圆O的两条切线,A,B是切点,C是劣弧AB(不包括端点)上一点,直线PC交圆O于另一点D,Q在弦CD上,且∠DAQ=∠PBC.求证: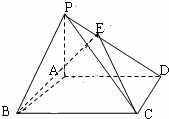 (理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.
(理科)已知如图,四边形ABCD是矩形,PA⊥面ABCD,其中AB=3,PA=4.若在PD上存在一点E,使得BE⊥CE.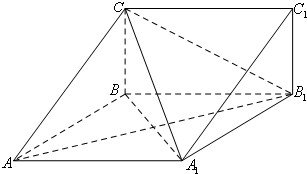 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=45°,四边形BCC1B1为矩形,若AC=5,AB=4,BC=3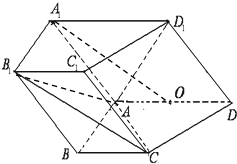 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=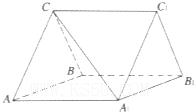 如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.
如图,三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°.