题目内容
9．三棱锥A-BCD中，AB，AC，AD两两垂直，其外接球半径为2，设三棱锥A-BCD的侧面积为S，则S的最大值为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 16 |
分析 三棱锥A-BCD的三条侧棱两两互相垂直，所以把它扩展为长方体，它也外接于球，对角线的长为球的直径，然后利用基本不等式解答即可．
解答 解：设AB，AC，AD分别为a，b，c，则三棱锥A-BCD的三条侧棱两两互相垂直，所以把它扩展为长方体，
它也外接于球，对角线的长为球的直径，∴a2+b2+c2=16，
S=$\frac{1}{2}$（ab+bc+ac）≤$\frac{1}{2}$（a2+b2+c2）=8，
故选C．
点评 本题考查三棱锥A-BCD的侧面积，考查学生空间想象能力，解答的关键是构造球的内接长方体，是基础题．
练习册系列答案
相关题目
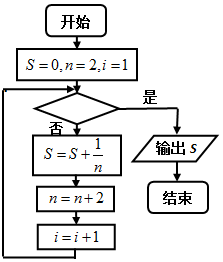如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图，其中判断框内应填入的条件是（ ）
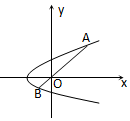在抛物线y2=4a（x+a）（a＞0），设有过原点O作一直线分别交抛物线于A、B两点，如图所示，试求|OA|•|OB|的最小值．
在图所示的几何体中，底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD=AD=2EC=2，N为线段PB的中点．