题目内容
4.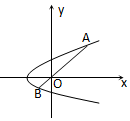 在抛物线y2=4a(x+a)(a>0),设有过原点O作一直线分别交抛物线于A、B两点,如图所示,试求|OA|•|OB|的最小值.
在抛物线y2=4a(x+a)(a>0),设有过原点O作一直线分别交抛物线于A、B两点,如图所示,试求|OA|•|OB|的最小值.
分析 直线AB的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$(α为参数),代入y2=4a(x+a)中得:t2sin2α-4atcosα-4a2=0,即可求|OA|•|OB|的最小值.
解答 解:直线AB的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$(α为参数),
代入y2=4a(x+a)中得:t2sin2α-4atcosα-4a2=0,
∴|OA||OB|=|t1t2|=$\frac{4{a}^{2}}{si{n}^{2}α}$≥4a2,
∴|OA|•|OB|的最小值为4a2.
点评 本题考查参数方程的运用,考查参数的几何意义,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
19.对实数a与b,定义新运算“?”:a?b=$\left\{\begin{array}{l}{a,a-b≤1}\\{b,a-b>1}\end{array}\right.$.设函数f(x)=(x2-2)?(x-x2),x∈R.若函数y=f(x)-c的零点恰有两个,则实数c的取值范围是( )
| A. | (-∞,-2]∪(-1,$\frac{3}{2}$) | B. | (-∞,-2]∪(-1,-$\frac{3}{4}$) | C. | (-∞,$\frac{1}{4}$)∪($\frac{1}{4}$,+∞) | D. | (-1,-$\frac{3}{4}$)∪[$\frac{1}{4}$,+∞) |
16.执行如图所示的程序框图,则输出s的值为( )
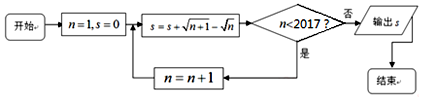

| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
14.某人的身份证号码是340304199803041290,随机掷一枚骰子,出现的点数是身份证上的数字的概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |