题目内容

19．复数z在复平面内对应的点是（1，-1），则$\overline{z}$=1+i．

分析 由已知求得z，再由共轭复数的概念得答案．

解答 解：∵复数z在复平面内对应的点是（1，-1），
∴z=1-i，则$\overline{z}=1+i$．
故答案为：1+i．

点评 本题考查复数的代数表示法及其几何意义，考查共轭复数的概念，是基础题．

练习册系列答案
相关题目
9．已知命题$p：?x∈（{0，+∞}），lnx≥2\frac{x-1}{x+1}$，则￢p为（　　）
A．$?{x_0}∈（{0，+∞}），lnx≥2\frac{x-1}{x+1}$B．$?{x_0}∈（{0，+∞}），lnx＜2\frac{x-1}{x+1}$
C．$?x∈（{0，+∞}），lnx＜2\frac{x-1}{x+1}$D．不存在${x_0}∈（{0，+∞}），lnx＜2\frac{x-1}{x+1}$
10．设实数x，y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-y≤0}\\{x+3y≤3}\end{array}\right.$，则$\frac{x-y}{\sqrt{{x}^{2}+{y}^{2}}}$的取值范围是[$-\sqrt{2}$，-1）∪（-1，0]．
7．已知直线y=k（x+1）（k＞0）与抛物线C：y2=4x相交于A，B两点，O、F分别为C的顶点和焦点，若$\overrightarrow{OA}$=λ$\overrightarrow{FB}$（λ∈R），则k=$\frac{2\sqrt{2}}{3}$．
14．已知圆C：（x+1）2+y2=12及点F（1，0）点，P在圆上，M，N分别为PF、PC上的点，且满足$\overrightarrow{PM}$=$\overrightarrow{MF}$，$\overrightarrow{MN}$•$\overrightarrow{PF}$=0
（1）求N的轨迹W的方程；
（2）是否存在过点F（1，0）的直线l与曲线W相交于A，B两点，并且与曲线W上一点Q，使得四边形OAQB为平行四边形？若存在，求出直线l的方程；若不存在，说明理由．
4．在△ABC中，内角A、B、C所对的边分别为a、b、c，已知a≠b，cos2A-cos2B=$\sqrt{3}$sinAcosA-$\sqrt{3}$sinBcosB．
（Ⅰ）求角C的大小；
（Ⅱ）若c=$\sqrt{3}$，siniA=$\frac{\sqrt{2}}{2}$，求△ABC的面积．
11．函数$f（x）=\sqrt{\frac{1}{4}{x^2}-1}+{x^2}-9$的零点个数为（　　）
A．0B．2C．4D．6
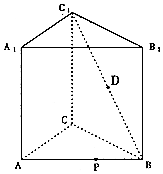8．如图，正三棱柱ABC-A1B1C1中，AB=2，AA1=3，D为C1B的中点，P为AB边上的动点．
（1）当点P为AB的中点时，证明：DP∥平面ACC1A1；
（2）若AP=3PB，求三棱锥B-CDP的体积；
（3）求二面角C-A1D-A的余弦值．
9．三棱锥A-BCD中，AB，AC，AD两两垂直，其外接球半径为2，设三棱锥A-BCD的侧面积为S，则S的最大值为（　　）
A．4B．6C．8D．16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网