题目内容
19．《九章算术•衰分》是我国古代内容极为丰富的数学名著，书中有如下问题：今有禀栗，大夫、不更、簪裹、上造、公士、凡五人，一十五斗，今有大夫一人后来，亦当禀五斗，仓无栗，欲以衰出之，问各几何？
现解决如下问题：原有大夫、不更、簪裹、上造、公士5种爵位各1人，现增加一名大夫，共计6人，按照爵位共献出5斗栗，其中5种爵位的人所献“禀栗”成等差数列{an}，其公差d满足d=-a5，请问6人中爵位为“簪裹”的人需献出栗的数量是（ ）
| A． | $\frac{3}{4}$斗 | B． | $\frac{4}{5}$斗 | C． | 1斗 | D． | $\frac{5}{4}$斗 |
分析 利用率等差数列的通项公式列出方程组，求出首项和公差，由此能求出结果．
解答 解：由题意得：
$\left\{\begin{array}{l}{2{a}_{1}+{a}_{1}-{a}_{5}+{a}_{1}-2{a}_{5}+{a}_{1}-3{a}_{5}+{a}_{1}-4{a}_{5}=5}\\{{a}_{1}=-（{a}_{1}+4d）}\end{array}\right.$，
解得${a}_{1}=\frac{5}{4}，d=-\frac{1}{4}$，
∴6人中爵位为“簪裹”的人需献出栗的数量是a3=a1+2d=$\frac{5}{4}-\frac{2}{4}$=$\frac{3}{4}$（斗）．
故选：A．
点评 本题考查了等差数列的通项公式，考查了等差数列的前n项和，是基础题．
练习册系列答案
相关题目
7．
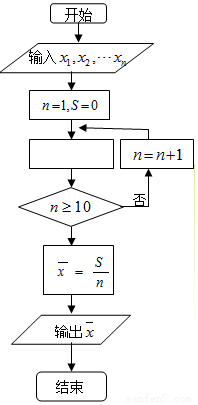如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图，图中空白框中应填入的内容为（ ）
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图，图中空白框中应填入的内容为（ ）| A． | S=S+xn | B． | S=S+$\frac{{x}_{n}}{n}$ | C． | S=S+n | D． | S=S+$\frac{{x}_{n}}{10}$ |
14．某人的身份证号码是340304199803041290，随机掷一枚骰子，出现的点数是身份证上的数字的概率为（ ）
| A． | $\frac{2}{9}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{6}$ |
11．某工厂拟生产甲、乙两种实销产品．已知每件甲产品的利润为0.4万元，每件乙产品的利润为0.3万元，两种产品都需要在A，B两种设备上加工，且加工一件甲、乙产品在A，B设备上所需工时（单位：h）分别如表所示．
若A设备每月的工时限额为400h，B设备每月的工时限额为300h，则该厂每月生产甲、乙两种产品可获得的最大利润为（ ）
| 甲产品所需工时 | 乙产品所需工时 | |
| A设备 | 2 | 3 |
| B设备 | 4 | 1 |
| A． | 40万元 | B． | 45万元 | C． | 50万元 | D． | 55万元 |
8．
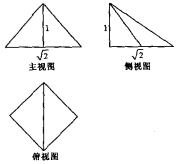刘徽的《九章算术注》中有这样的记载：“邪解立方有两堑堵，邪解堑堵，其一为阳马，一为鳖臑，阳马居二，鳖臑居一，不易之率也．”意思是说：把一块立方体沿斜线分成相同的两块，这两块叫做堑堵，再把一块堑堵沿斜线分成两块，大的叫阳马，小的叫鳖臑，两者体积比为2：1，这个比率是不变的，如图是一个阳马的三视图，则其表面积为（ ）
刘徽的《九章算术注》中有这样的记载：“邪解立方有两堑堵，邪解堑堵，其一为阳马，一为鳖臑，阳马居二，鳖臑居一，不易之率也．”意思是说：把一块立方体沿斜线分成相同的两块，这两块叫做堑堵，再把一块堑堵沿斜线分成两块，大的叫阳马，小的叫鳖臑，两者体积比为2：1，这个比率是不变的，如图是一个阳马的三视图，则其表面积为（ ）| A． | 2 | B． | 2+$\sqrt{2}$ | C． | 3+$\sqrt{3}$ | D． | 3+$\sqrt{2}$ |