题目内容
(文科)设函数f(x)=x2-2ax-8a2(a>0),记不等式f(x)≤0的解集为A.
(1)当a=1时,求集合A;
(2)若(-1,1)⊆A,求实数a的取值范围.
(1)当a=1时,求集合A;
(2)若(-1,1)⊆A,求实数a的取值范围.
考点:集合的包含关系判断及应用
专题:集合
分析:(1)当a=1时,f(x)=x2-2x-8,不等式x2-2x-8≤0,化为(x-4)(x+2)≤0,解出即可.
(2)由x2-2ax-8a2≤0,可得(x-4a)(x+2a)≤0,由于a>0,可得-2a≤x≤4a,即A=[-2a,4a].由于(-1,1)⊆A,可得
,解得即可.
(2)由x2-2ax-8a2≤0,可得(x-4a)(x+2a)≤0,由于a>0,可得-2a≤x≤4a,即A=[-2a,4a].由于(-1,1)⊆A,可得
|
解答:
解:(1)当a=1时,f(x)=x2-2x-8,
由不等式x2-2x-8≤0,化为(x-4)(x+2)≤0,
解得-2≤x≤4,
∴集合A={x|-2≤x≤4}.
(2)∵x2-2ax-8a2≤0,
∴(x-4a)(x+2a)≤0,
又∵a>0,∴-2a≤x≤4a,∴A=[-2a,4a].
又∵(-1,1)⊆A,
∴
,解得a≥
,
∴实数a的取值范围是[
,+∞).
由不等式x2-2x-8≤0,化为(x-4)(x+2)≤0,
解得-2≤x≤4,
∴集合A={x|-2≤x≤4}.
(2)∵x2-2ax-8a2≤0,
∴(x-4a)(x+2a)≤0,
又∵a>0,∴-2a≤x≤4a,∴A=[-2a,4a].
又∵(-1,1)⊆A,
∴
|
| 1 |
| 2 |
∴实数a的取值范围是[
| 1 |
| 2 |
点评:本题考查了一元二次不等式的解法、集合之间的关系,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
已知sinαcosα=
,且π<α<
,则cosα-sinα的值为( )
| 1 |
| 8 |
| 5π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
下列三角函数值:
①sin(nπ+
π)(n∈Z);
②sin(2nπ+
)(n∈Z);
③sin[(2n+1)π-
](n∈Z),
其中,函数值与sin
的值相同的是( )
①sin(nπ+
| 4 |
| 3 |
②sin(2nπ+
| π |
| 3 |
③sin[(2n+1)π-
| π |
| 3 |
其中,函数值与sin
| π |
| 3 |
| A、①② | B、③ | C、②③ | D、② |
若直线l不平行于平面 α,且l?α,则( )
| A、α内不存在与l平行的直线 |
| B、α内的所有直线与l异面 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
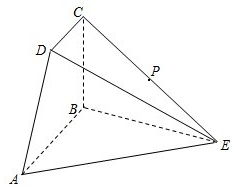 如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,AB=2CD=2BC=2,P为CE中点.
如图所示,四边形ABCD为直角梯形,AB∥CD,AB⊥BC,△ABE为等边三角形,且平面ABCD⊥平面ABE,AB=2CD=2BC=2,P为CE中点.