题目内容
设函数f（x）=x2-kx+b，其中k，b为实数．
（Ⅰ）当b=6时，不等式f（x）＜0的解集为{x|2＜x＜m}，求实数k及m的值；
（Ⅱ）当b=2时，是否存在实数k，使得不等式f（sinx）≥k-1对任意的实数x∈[0，
]恒成立？若存在，求k的取值范围；若不存在，请说明理由．
（Ⅰ）当b=6时，不等式f（x）＜0的解集为{x|2＜x＜m}，求实数k及m的值；
（Ⅱ）当b=2时，是否存在实数k，使得不等式f（sinx）≥k-1对任意的实数x∈[0，
| π |
| 2 |
考点：二次函数的性质
专题：计算题,函数的性质及应用
分析：（Ⅰ）当b=6时，由题意x=2是方程f（x）=0的根，所以k=5，再利用韦达定理可求m的值；
（Ⅱ）当b=2时，存在实数k，使得不等式f（sinx）≥k-1对任意的实数x∈[0，
]恒成立，等价于k≤
．求出右边的最值，即可求出k的取值范围．
（Ⅱ）当b=2时，存在实数k，使得不等式f（sinx）≥k-1对任意的实数x∈[0，
| π |
| 2 |
| sin2x+3 |
| sinx+1 |
解答：
解：（Ⅰ）当b=6时，由题意x=2是方程f（x）=0的根，所以k=5；
k=5时，2+m=5，所以m=3；
（Ⅱ）当b=2时，存在实数k，使得不等式f（sinx）≥k-1对任意的实数x∈[0，
]恒成立，
等价于k≤
．
令g（x）=
，则g（x）=（sinx+1）+
-2≥2，
∵x∈[0，
]，∴1≤sinx+1≤2，当且仅当sinx=1时，g（x）取最小值2，
∴k的取值范围是（-∞，2]．
k=5时，2+m=5，所以m=3；
（Ⅱ）当b=2时，存在实数k，使得不等式f（sinx）≥k-1对任意的实数x∈[0，
| π |
| 2 |
等价于k≤
| sin2x+3 |
| sinx+1 |
令g（x）=
| sin2x+3 |
| sinx+1 |
| 4 |
| sinx+1 |
∵x∈[0，
| π |
| 2 |
∴k的取值范围是（-∞，2]．
点评：本题考查二次不等式的解法，考查恒成立问题，考查学生分析解决问题的能力，难度中等．
练习册系列答案
相关题目
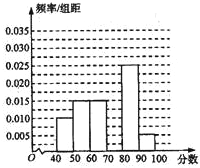某校高一年级有2000名学生，从中随机抽出60名学生，将这60名学生的某次数学考试成绩（百分制）分成六段[40，50），[50，60），…，[90，100]后，得到如图所示的频率分布直方图，观察图形的信息，回答下列问题：
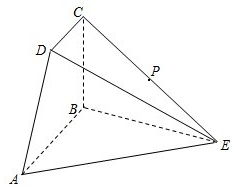如图所示，四边形ABCD为直角梯形，AB∥CD，AB⊥BC，△ABE为等边三角形，且平面ABCD⊥平面ABE，AB=2CD=2BC=2，P为CE中点．
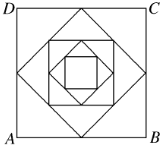如图，正方形ABCD的边长是a，依次连接正方形ABCD各边中点得到一个新的正方形，再依次连接新正方形各边中点又得到一个新的正方形，依此得到一系列的正方形，如图所示．现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个正方形的边逆时针方向爬行，如此下去，问爬行2n条线段的长度的平方和是多少？