题目内容
已知函数f(x)=ex-1-x.
(Ⅰ)求f(x)的最小值;
(Ⅱ)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设g(x)=(f′(x)+1)(x2-1),试问函数g(x)在(1,+∞)上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
(Ⅰ)求f(x)的最小值;
(Ⅱ)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间.设g(x)=(f′(x)+1)(x2-1),试问函数g(x)在(1,+∞)上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)求导数,确定函数的单调性,即可求f(x)的最小值;
(Ⅱ)假设函数g(x)存在保值区间[a,b],可得方程(x2-1)ex=x有两个大于1的相异实根.设φ(x)=(x2-1)ex-x(x>1),证明φ(x)在(1,+∞)上单增,可得φ(x)在区间(1,+∞)上至多有一个零点,与方程(x-1)2ex=x有两个大于1的相异实根矛盾,即可得出结论.
(Ⅱ)假设函数g(x)存在保值区间[a,b],可得方程(x2-1)ex=x有两个大于1的相异实根.设φ(x)=(x2-1)ex-x(x>1),证明φ(x)在(1,+∞)上单增,可得φ(x)在区间(1,+∞)上至多有一个零点,与方程(x-1)2ex=x有两个大于1的相异实根矛盾,即可得出结论.
解答:
解:(Ⅰ)求导数,得f'(x)=ex-1.
令f'(x)=0,解得x=0. …(2分)
当x<0时,f'(x)<0,所以f(x)在(-∞,0)上是减函数;
当x>0时,f'(x)>0,所以f(x)在(0,+∞)上是增函数.
故f(x)在x=0处取得最小值f(0)=0. …(6分)
(Ⅱ)函数g(x)在(1,+∞)上不存在保值区间,证明如下:
假设函数g(x)存在保值区间[a,b],
由g(x)=(x2-1)ex得:g'(x)=(x2+2x-1)ex
因x>1时,g'(x)>0,所以g(x)为增函数,所以
即方程(x2-1)ex=x有两个大于1的相异实根 …(9分)
设φ(x)=(x2-1)ex-x(x>1),则φ'(x)=(x2+2x-1)ex-1
因x>1,φ'(x)>0,所以φ(x)在(1,+∞)上单增
所以φ(x)在区间(1,+∞)上至多有一个零点 …(12分)
这与方程(x-1)2ex=x有两个大于1的相异实根矛盾
所以假设不成立,即函数h(x)在(1,+∞)上不存在保值区间.…(13分)
令f'(x)=0,解得x=0. …(2分)
当x<0时,f'(x)<0,所以f(x)在(-∞,0)上是减函数;
当x>0时,f'(x)>0,所以f(x)在(0,+∞)上是增函数.
故f(x)在x=0处取得最小值f(0)=0. …(6分)
(Ⅱ)函数g(x)在(1,+∞)上不存在保值区间,证明如下:
假设函数g(x)存在保值区间[a,b],
由g(x)=(x2-1)ex得:g'(x)=(x2+2x-1)ex
因x>1时,g'(x)>0,所以g(x)为增函数,所以
|
即方程(x2-1)ex=x有两个大于1的相异实根 …(9分)
设φ(x)=(x2-1)ex-x(x>1),则φ'(x)=(x2+2x-1)ex-1
因x>1,φ'(x)>0,所以φ(x)在(1,+∞)上单增
所以φ(x)在区间(1,+∞)上至多有一个零点 …(12分)
这与方程(x-1)2ex=x有两个大于1的相异实根矛盾
所以假设不成立,即函数h(x)在(1,+∞)上不存在保值区间.…(13分)
点评:本题考查导数知识的运用,考查函数的单调性与最值,考查新定义,考查小时分析解决问题的能力,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
在下列四个命题中
①y=1是幂函数;
②“x<1”是“x<2”的充分不必要条件;
③命题“存在x∈R,x2-2>0”的否定是:“任意x∈R,x2-x<0”
④若a=-1,则函数f(x)=ax2+2x-1只有一个零点.
其中错误的个数有( )个.
①y=1是幂函数;
②“x<1”是“x<2”的充分不必要条件;
③命题“存在x∈R,x2-2>0”的否定是:“任意x∈R,x2-x<0”
④若a=-1,则函数f(x)=ax2+2x-1只有一个零点.
其中错误的个数有( )个.
| A、4 | B、2 | C、3 | D、1 |
下列有关命题的说法正确的是( )
| A、命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0 |
| B、命题“矩形是平行四边形”的否定为真命题 |
| C、命题“若cosx=cosy,则x=y”的逆否命题为真命题 |
| D、命题“若x+y=0,则x,y互为相反数”的逆命题为真命题 |
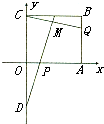 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=