题目内容
3．执行如图所示的程序框图，则输出的结果为（ ）
| A． | 7 | B． | 9 | C． | 10 | D． | 11 |
分析 根据框图的流程依次运行程序，直到满足条件s＜0.1，确定输出的i值即可得解．
解答 解：模拟程序的运行，可得
i=1，s=1
s=$\frac{1}{3}$，
不满足条件s＜0.1，执行循环体，i=3，s=$\frac{1}{5}$，
不满足条件s＜0.1，执行循环体，i=5，s=$\frac{1}{7}$，
不满足条件s＜0.1，执行循环体，i=7，s=$\frac{1}{9}$，
不满足条件s＜0.1，执行循环体，i=9，s=$\frac{1}{11}$，
满足条件s＜0.1，退出循环，输出i的值为9．
故选：B．
点评 本题考查了循环结构的程序框图，根据框图的流程依次运行程序是解答此类问题的常用方法，属于基础题．
练习册系列答案
相关题目
6．设$\overrightarrow{a}$，$\overrightarrow{b}$是非零向量，则“$\overrightarrow{a}$，$\overrightarrow{b}$共线”是“|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|”的（ ）
| A． | 充分而不必要条件 | B． | 必要而不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
7．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点分别为F1，F2，第二象限的点P（x0，y0）满足bx0+ay0=0，若线段PF2的垂直平分线恰为双曲线C的过一、三象限的渐近线，则双曲线C的离心率为（ ）
| A． | $\sqrt{5}$ | B． | 4 | C． | $\sqrt{3}$ | D． | 2 |
18．设集合A={0，1}，B={x|x2+x-2=0}，则A∪B=（ ）
| A． | ∅ | B． | {1} | C． | {-2，0，1} | D． | {-1，0，1，2} |
8．
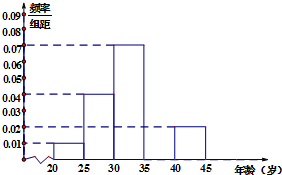当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：
（1）求出表中的a，b，n的值，并补全频率分布直方图；
（2）媒体记者为了做好调查工作，决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访，再从抽出的这20名中年龄在[30，40）的选取2名担任主要发言人．记这2名主要发言人年龄在[35，40）的人数为ξ，求ξ的分布列及数学期望．
当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：| 组数 | 分组（单位：岁） | 频数 | 频率 |
| 1 | [20，25） | 5 | 0.05 |
| 2 | [25，30） | 20 | 0.20 |
| 3 | [30，35） | a | 0.35 |
| 4 | [35，40） | 30 | b |
| 5 | [40，45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
（2）媒体记者为了做好调查工作，决定从所随机抽取的市民中按年龄采用分层抽样的方法抽取20名接受采访，再从抽出的这20名中年龄在[30，40）的选取2名担任主要发言人．记这2名主要发言人年龄在[35，40）的人数为ξ，求ξ的分布列及数学期望．
15．当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：
（1）求出表中的a，b的值，并补全频率分布直方图；
（2）媒体记者为了做好调查工作，决定在第2，4，5组中用分层抽样的方法抽取6名市民进行问卷调查，再从这6名市民中随机抽取2名接受电视采访，求第2组至少有一名接受电视采访的概率？
当今，手机已经成为人们不可或缺的交流工具，人们常常把喜欢玩手机的人冠上了名号“低头族”，手机已经严重影响了人们的生活，一媒体为调查市民对低头族的认识，从某社区的500名市民中，随机抽取n名市民，按年龄情况进行统计的得到频率分布表和频率分布直方图如下：| 组数 | 分组（单位：岁） | 频数 | 频率 |
| 1 | [20，25） | 5 | 0.05 |
| 2 | [25，30） | 20 | 0.20 |
| 3 | [30，35） | a | 0.35 |
| 4 | [35，40） | 30 | b |
| 5 | [40，45] | 10 | 0.10 |
| 合计 | n | 1.00 | |
（2）媒体记者为了做好调查工作，决定在第2，4，5组中用分层抽样的方法抽取6名市民进行问卷调查，再从这6名市民中随机抽取2名接受电视采访，求第2组至少有一名接受电视采访的概率？