题目内容
设△ABC的内角为A、B、C所对边的长分别是a、b、c，且b=3，c=1，A=2B．
（Ⅰ）求a的值；
（Ⅱ）求sin（A+
）的值．
（Ⅰ）求a的值；
（Ⅱ）求sin（A+
| π |
| 4 |
考点：正弦定理,两角和与差的正弦函数
专题：综合题,三角函数的求值
分析：（Ⅰ）利用正弦定理，可得a=6cosB，再利用余弦定理，即可求a的值；
（Ⅱ）求出sinA，cosA，即可求sin（A+
）的值．
（Ⅱ）求出sinA，cosA，即可求sin（A+
| π |
| 4 |
解答：
解：（Ⅰ）∵A=2B，
=
，b=3，
∴a=6cosB，
∴a=6•
，
∴a=2
；
（Ⅱ）∵a=6cosB，
∴cosB=
，
∴sinB=
，
∴sinA=sin2B=
，cosA=cos2B=2cos2B-1=-
，
∴sin（A+
）=
（sinA+cosA）=
．
| a |
| sinA |
| b |
| sinB |
∴a=6cosB，
∴a=6•
| a2+1-9 |
| 2a |
∴a=2
| 3 |
（Ⅱ）∵a=6cosB，
∴cosB=
| ||
| 3 |
∴sinB=
| ||
| 3 |
∴sinA=sin2B=
2
| ||
| 3 |
| 1 |
| 3 |
∴sin（A+
| π |
| 4 |
| ||
| 2 |
4-
| ||
| 6 |
点评：本题考查余弦定理、考查正弦定理，考查二倍角公式，考查学生的计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
若log4（3a+4b）=log2
，则a+b的最小值是（ ）
| ab |
A、6+2
| ||
B、7+2
| ||
C、6+4
| ||
D、7+4
|
如图，点A为圆外一点，过点A作圆的两条切线，切点分别为B，C，ADE是圆的割线，连接CD，BD，BE，CE．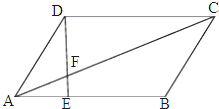
如图，在平行四边形ABCD中，点E在AB上且EB=2AE，AC与DE交于点F，则