题目内容
曲线f（x）=ex在点A（1，f（1））处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的概念及应用
分析：先求切点，然后对函数求导，根据导数的几何意义可知函数f（x）在x=1处的切线斜率k=f′（1），利用点斜式可求直线方程．
解答：
解：∵f（x）=ex
∴f（1）=e且f′（x）=ex
根据导数的几何意义可知函数f（x）在x=1处的切线斜率k=f′（1）=e
∴函数f（x）=ex在x=1处的切线方程是y-e=e（x-1），
即y=ex
故答案为：y=ex．
∴f（1）=e且f′（x）=ex
根据导数的几何意义可知函数f（x）在x=1处的切线斜率k=f′（1）=e
∴函数f（x）=ex在x=1处的切线方程是y-e=e（x-1），
即y=ex
故答案为：y=ex．
点评：本题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
已知函数f（x）=x2-4，点A1（x1，0），过点A1作x轴的垂线交抛物线C：y=f（x）于点B1，过B1作抛物线C：y=f（x）的切线与x轴交于点A2（x2，0），过点A2作x轴的垂线交抛物线C：y=f（x）于点B2，过点B2作抛物线C：y=f（x）的切线交x轴于点A3（x3，0）┉依次下去，得到x1、x2、x3┉，xn，其中x1＞0，函数y=x3-x2-x的单调递增区间为（ ）
A、(-∞，-
| ||
B、[-
| ||
C、(-∞，-
| ||
D、[-1，
|
某个实心零部件的形状是如图所示的几何体，其下部是底面均是正方形，侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD，上面是一个底面与四棱台的上底面重合，侧面是全等的矩形的四棱柱ABCD-A2B2C2D2．现需要对该零部件表面进行防腐处理，已知AB=10，A1B1=20，AA2=30，AA1=13（单位：厘米），每平方厘米的加工处理费为0.20元，需加工处理费多少元？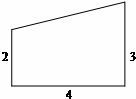
在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角 梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是