题目内容
某个实心零部件的形状是如图所示的几何体，其下部是底面均是正方形，侧面是全等的等腰梯形的四棱台A1B1C1D1-ABCD，上面是一个底面与四棱台的上底面重合，侧面是全等的矩形的四棱柱ABCD-A2B2C2D2．现需要对该零部件表面进行防腐处理，已知AB=10，A1B1=20，AA2=30，AA1=13（单位：厘米），每平方厘米的加工处理费为0.20元，需加工处理费多少元？考点：组合几何体的面积、体积问题
专题：计算题
分析：求出几何体的表面积，然后求解加工费用．
解答：
解：∵四棱柱ABCD-A2B2C2D2的底面是正方形，侧面是全等的矩形，
∴S1=SA2B2C2D2+S四个侧面=(A2B2)2+4AB•AA2=102+4×10×30=1300(cm2)….4′
因为四棱台A1B1C1D1-ABCD的上、下底面均是正方形，侧面是全等的等腰梯形，所以S2=SA1B1C1D1+S四个侧面梯形=(A1B1)2+4×
(AB+A1B1)h等腰梯形的高=202+4×
(10+20)
=1120(cm2)…8′
于是该实心零部件的表面积为S=S1+S2=1300+1120=2420(cm2)，
故所需加工处理费为0.2S=0.2×2420=484（元） ….12′
∴S1=SA2B2C2D2+S四个侧面=(A2B2)2+4AB•AA2=102+4×10×30=1300(cm2)….4′
因为四棱台A1B1C1D1-ABCD的上、下底面均是正方形，侧面是全等的等腰梯形，所以S2=SA1B1C1D1+S四个侧面梯形=(A1B1)2+4×
| 1 |
| 2 |
| 1 |
| 2 |
132-[
|
于是该实心零部件的表面积为S=S1+S2=1300+1120=2420(cm2)，
故所需加工处理费为0.2S=0.2×2420=484（元） ….12′
点评：本题考查几何体的表面积的求法，注意几何体的侧面积公式的应用，考查计算能力．
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
已知x，y满足
，且z=2x-y的最大值是最小值的4倍，则a的值是（ ）
|
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
已知受限制的二次函数y=f（x），x∈[-1，2]，f（0）=2，f（1）=0，f(
)=
，则该函数的值域为（ ）
| 1 |
| 2 |
| 3 |
| 4 |
| A、[0，6] | ||
B、[-
| ||
C、[-
| ||
D、(-
|
如图，已知球O的面上有四点A，B，C，D，DA⊥平面ABC，AB⊥BC，DA=AB=BC=2，则球O的体积与表面积的比为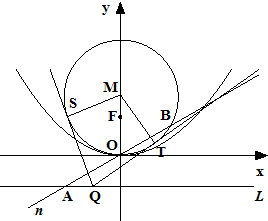
已知抛物线C：x2=2py（p＞0）的准线为L，焦点为F，⊙M的圆心在y轴的正半轴上，且与x轴相切，过原点作倾斜角为