题目内容
8.若函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.(1)写出函数f(x)(x∈R)的解析式.
(2)若函数g(x)=f(x)+(4-2a)x+2(x∈[1,2]),求函数g(x)的最小值h(a).
(3)若f(x)≤-2at+4对于任意的x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
分析 (1)设x>0,则-x<0,利用已知函数解析式和函数的奇偶性可得x>0时的解析式,则答案可求;
(2)求出函数g(x),找出对称轴方程,对a分类求得函数的最小值;
(3)把f(x)≤-2at+4对于任意的x∈[-1,1],a∈[-1,1]恒成立,转化为0≤-2at+4,进一步转化为关于t的不等式组得答案.
解答 解:(1)设x>0,则-x<0,
又函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=(-x)2-2x=x2-2x.
∴$f(x)=\left\{\begin{array}{l}{x^2}-2x,x>0\\{x^2}+2x,x≤0.\end{array}\right.$;
(2)g(x)=f(x)+(4-2a)x+2=x2+2x-2ax+2(1≤x≤2),对称轴方程为:x=a-1,
当a-1≤1 时,g(1)=5-2a为最小;
当1<a-1≤2时,g(a-1)=-a2+2a+1为最小;
当a-1>2时,g(2)=10-4a为最小.
综上:h(a)=$\left\{\begin{array}{l}{5-2a,a≤2}\\{-{a}^{2}+2a+1,2<a≤3}\\{10-4a,a>3}\end{array}\right.$;
(3)f(x)≤-2at+4对于任意的x∈[-1,1],a∈[-1,1]恒成立,
即0≤-2at+4,也就是2ta-4≤0,a∈[-1,1]恒成立,
∴$\left\{\begin{array}{l}{-2t-4≤0}\\{2t-4≤0}\end{array}\right.$,解得:-2≤t≤2.
点评 本题考查函数解析式的求解及常用方法,考查数学转化思想方法,训练了恒成立问题的求解方法,是中档题.

练习册系列答案
相关题目
4.为响应“精确扶贫”号召,某企业计划每年用不超过100万元的资金购买单价分别为1500元/箱和3000元/箱的A、B两种药品捐献给贫困地区某医院,其中A药品至少100箱,B药品箱数不少于A药品箱数.则该企业捐献给医院的两种药品总箱数最多可为( )
| A. | 200 | B. | 350 | C. | 400 | D. | 500 |
5.民大附中的甲、乙两人同时参加某大学的自主招生,在申请材料中提交了某学科10次的考试成绩(满分100分),按照时间顺序记录如下:

(1)根据两组数据画出两人成绩的茎叶图,并通过茎叶图比较两人成绩的平均值及分散程度(不要求计算具体值,直接写出结论即可);
(2)现将两人成绩分为三个等级:
注:A级高于B级,B级高于C级
假设两人的成绩相互独立,根据所给的数据,以事件发生的频率为相应事件发生的概率,求甲的等级高于乙的等级的概率;
(3)假如你是该大学的招生老师,结合上述数据,决定应录取哪位同学,说明理由.

(1)根据两组数据画出两人成绩的茎叶图,并通过茎叶图比较两人成绩的平均值及分散程度(不要求计算具体值,直接写出结论即可);
(2)现将两人成绩分为三个等级:
| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
假设两人的成绩相互独立,根据所给的数据,以事件发生的频率为相应事件发生的概率,求甲的等级高于乙的等级的概率;
(3)假如你是该大学的招生老师,结合上述数据,决定应录取哪位同学,说明理由.
16.已知集合A={x|2x>1},集合B={x||x|≤2},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [-2,2] | D. | (-2,2) |
20.命题p:?x∈R,x2+ax+a2≥0;命题q:?x∈R,sinx+cosx=2,则下列命题中为真命题的是( )
| A. | (¬p)∧(¬q) | B. | p∧q | C. | (¬p)∨q | D. | p∧(¬q) |
18.设$a={log_{\frac{1}{3}}}\frac{1}{2},b={log_{\frac{1}{2}}}\frac{1}{3},c={log_3}\frac{4}{3}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | b<c<a |
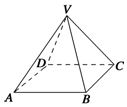 如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.