题目内容
17.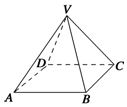 如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥VABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
分析 连结AC,BD,交于点O,连结VO,先求出高VO,由此能求出这个正四棱锥的体积.
解答 解:连结AC,BD,交于点O,连结VO,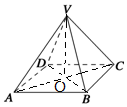
∵四棱锥VABCD的底面为边长等于2cm的正方形,
顶点V与底面正方形中心的连线为棱锥的高,
侧棱长VC=4cm,
∴AO=$\frac{1}{2}\sqrt{4+4}$=$\sqrt{2}$(cm),
∴VO=$\sqrt{16-2}$=$\sqrt{14}$(cm),
∴这个正四棱锥的体积:
V=$\frac{1}{3}{S}_{正方形ABCD}×VO$=$\frac{1}{3}×2×2×\sqrt{14}$=$\frac{4\sqrt{14}}{3}$(cm3).
点评 本题考查四棱锥的体积的求法,考查推理论证能力、空间思维能力、运算求解能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
2.如图是某四棱锥的三视图,则该几何体的表面积等于( )
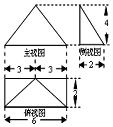

| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |
6.设函数f(x)=$\frac{1}{3}$x-lnx(x>0),则函数f(x)( )
| A. | 在区间(0,1)内有零点,在区间(1,+∞)内无零点 | |
| B. | 在区间(0,1)内有零点,在区间(1,+∞)内有零点 | |
| C. | 在区间(0,3),(3,+∞)均无零点 | |
| D. | 在区间(0,3),(3,+∞)均有零点 |
7.极坐标方程3ρsin2θ+cosθ=0表示的曲线是( )
| A. | 抛物线 | B. | 双曲线 | C. | 椭圆 | D. | 圆 |
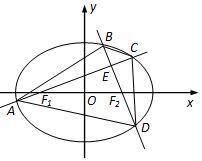 已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.
已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.