题目内容
13.已知曲线C的方程是:x2+y2-2x-4y+m=0,点P(3,-1).(1)若m=1,直线l过点P且与曲线C只有一个公共点,求直线l的方程;
(2)若曲线C表示圆且被直线x+2y+5=0截得的弦长为2$\sqrt{5}$,求实数m的值.
分析 (1)m=1时,曲线C表示圆,直线l过点P且与曲线C只有一个公共点,即直线l与圆相切,
①当直线l的斜率不存在时,直线l的方程为:x=3.
②当直线l的斜率存在时,设直线l的方程为:y=k(x-3)-1.由圆心到直线距离等于半径求得k.
(2)曲线C的方程配方得:(x-1)2+(y-2)2=5-m,若方程表示圆则m<5.
根据圆的弦长公式2$\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{5}$,⇒m的值.
解答 解:(1)m=1时,曲线C的方程是:(x-1)2+(y-2)2=4,
表示圆心为(1,2),半径为2的圆,
∵直线l过点P且与曲线C只有一个公共点,∴直线l与圆相切.
①当直线l的斜率不存在时,直线l的方程为:x=3.
②当直线l的斜率存在时,设直线l的方程为:y=k(x-3)-1.即kx-y-3k-1=0.
$\frac{|k-2-3k-1|}{\sqrt{{k}^{2}+1}}=2$⇒k=-$\frac{5}{12}$,直线l的方程为:5x+12y-3=0.
综上所述所求直线l的方程为:x=3,5x+12y-3=0.
(2)曲线C的方程配方得:(x-1)2+(y-2)2=5-m,若方程表示圆则5-m>0⇒m<5.
圆心到直线x+2y+5=0距离d=$\frac{10}{\sqrt{5}}=2\sqrt{5}$,
根据圆的弦长公式2$\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{5}$,⇒2$\sqrt{5-m-20}=2\sqrt{5}$,⇒m=-20
点评 本题考查了圆的方程、直线与圆的位置关系,弦长公式,属于中档题.

练习册系列答案
相关题目
4.sin20°sin10°-cos10°sin70°=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
1.若变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤2\\ x+y≥0\\ x≤4\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 2 | B. | 8 | C. | 5 | D. | 7 |
18.已知函数f(x)的定义域为[-2,2],且f(x)在[-2,2]上是增函数,f(1-m)<f(m),则实数m的取值范围为( )
| A. | $(\frac{1}{2},+∞)$ | B. | $(-∞,\frac{1}{2})$ | C. | $({\frac{1}{2},2}]$ | D. | $[{-2,\frac{1}{2}})$ |
2.如图是某四棱锥的三视图,则该几何体的表面积等于( )
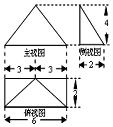

| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |