题目内容
5.民大附中的甲、乙两人同时参加某大学的自主招生,在申请材料中提交了某学科10次的考试成绩(满分100分),按照时间顺序记录如下:
(1)根据两组数据画出两人成绩的茎叶图,并通过茎叶图比较两人成绩的平均值及分散程度(不要求计算具体值,直接写出结论即可);
(2)现将两人成绩分为三个等级:
| 成绩分数 | [0,70] | [70,90] | [90,100] |
| 等级 | C级 | B级 | A级 |
假设两人的成绩相互独立,根据所给的数据,以事件发生的频率为相应事件发生的概率,求甲的等级高于乙的等级的概率;
(3)假如你是该大学的招生老师,结合上述数据,决定应录取哪位同学,说明理由.
分析 (1)以十位数为茎,个位数为叶,能作出茎叶图,由茎叶图知甲的平均成绩大于乙的平均成绩,甲的离散程度大于乙的离散程度.
(2)由已知得甲的10次成绩中,C级有5次,B级有3次,A级有2次,乙的10次成绩中,C级有7次,B级有2次,C级有1次,由此能求出甲的等级高于乙的等级的概率.
(3)假如我是该大学的招生老师,结合上述数据,我决定应录取甲同学,理由是同学平均成绩优于乙的平均成绩.
解答 解:(1)以十位数为茎,个位数为叶,作出茎叶图,如下图:
由茎叶图知甲的平均成绩大于乙的平均成绩,
甲的离散程度大于乙的离散程度.
(2)由已知得甲的10次成绩中,C级有5次,B级有3次,A级有2次,
乙的10次成绩中,C级有7次,B级有2次,C级有1次,
∴甲的等级高于乙的等级的概率p=$\frac{7}{10}×\frac{5}{10}+\frac{2}{10}×\frac{2}{10}$=0.39.
(3)假如我是该大学的招生老师,结合上述数据,
我决定应录取甲同学,
理由是甲同学平均成绩大于乙的平均成绩,
且甲同学达到B级和A级成绩标准的次数大于乙同学达到B级和A级成绩标准的次数.
点评 本题考查茎叶图的作法及应用,考查概率的求法,考查推理论证能力、运算求解能力,考查转化化归思想,是中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
16.三棱锥A-BCD内接于半径为2的球O,BC过球心O,当三棱锥A-BCD体积取得最大值时,三棱锥A-BCD的表面积为( )
| A. | $6+4\sqrt{3}$ | B. | $8+2\sqrt{3}$ | C. | $4+6\sqrt{3}$ | D. | $8+4\sqrt{3}$ |
4.sin20°sin10°-cos10°sin70°=( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
11.下列函数是奇函数且在(0,+∞)上单调递增的是( )
| A. | y=lnx | B. | y=x+$\frac{1}{x}$ | C. | y=x2 | D. | $y={x^{\frac{1}{3}}}$ |
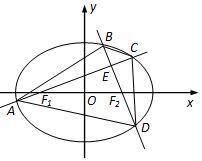 已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.
已知椭圆W:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右两个焦点为F1,F2,且|F1F2|=2,椭圆上一动点P满足|PF1|+|PF2|=2$\sqrt{3}$.