题目内容
3.已知等差数列{an}中,a2+a6=14,Sn为其前n项和,S5=25.(1)求{an}的通项公式;
(2)设${b_n}=\frac{2}{{{a_n}•{a_{n+1}}}}$,求数列{bn}的前n项和Tn的最小值.
分析 (1)利用已知条件求出数列的首项与公差,然后求解通项公式.
(2)化简通项公式的表达式,利用裂项消项法求解数列的和即可.
解答 解:(1)等差数列{an}中,a2+a6=14,Sn为其前n项和,S5=25.∴a3=5,
可得5-d+5+3d=14,解得d=2,则a1=1.
∴an=2n-1;
(2)由(1)知${b_n}=\frac{2}{{{a_n}{a_{n+1}}}}=\frac{2}{(2n-1)(2n+1)}=\frac{1}{2n-1}-\frac{1}{2n+1}$,${T_n}={b_1}+{b_2}+…+{b_n}=(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})$=$1-\frac{1}{2n+1}=\frac{2n}{2n+1}$,
所以Tn的最小值为$\frac{2}{3}$.
点评 本题考查数列的通项公式的应用,裂项法求解数列的和,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列函数是奇函数且在(0,+∞)上单调递增的是( )
| A. | y=lnx | B. | y=x+$\frac{1}{x}$ | C. | y=x2 | D. | $y={x^{\frac{1}{3}}}$ |
15.命题“若x=3,则x2-9x+18=0”的逆命题、否命题和逆否命题中,假命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
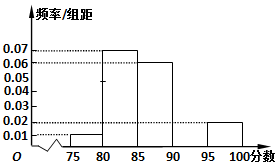 某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.