题目内容
12.在空间四边形ABCD中,$\overrightarrow{DA}=\overrightarrow a,\overrightarrow{DB}=\overrightarrow b,\overrightarrow{DC}=\overrightarrow c$,P在线段AD上,且DP=2PA,Q为BC的中点,则$\overrightarrow{PQ}$=( )| A. | $\frac{2}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b-\frac{1}{2}\overrightarrow c$ | B. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\frac{2}{3}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a-\frac{2}{3}\overrightarrow b+\frac{1}{2}\overrightarrow c$ | D. | $-\frac{2}{3}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
分析 由于$\overrightarrow{PQ}$=$\overrightarrow{PD}+\overrightarrow{DQ}$,$\overrightarrow{PD}$=-$\frac{2}{3}$$\overrightarrow{DA}$,$\overrightarrow{DQ}$=$\frac{1}{2}(\overrightarrow{DB}+\overrightarrow{DC})$,即可得出.
解答 解:$\overrightarrow{PQ}$=$\overrightarrow{PD}+\overrightarrow{DQ}$,$\overrightarrow{PD}$=-$\frac{2}{3}$$\overrightarrow{DA}$=-$\frac{2}{3}\overrightarrow{a}$,$\overrightarrow{DQ}$=$\frac{1}{2}(\overrightarrow{DB}+\overrightarrow{DC})$=$\frac{1}{2}$$(\overrightarrow{b}+\overrightarrow{c})$,
∴$\overrightarrow{PQ}$=-$\frac{2}{3}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\frac{1}{2}\overrightarrow{c}$.
点评 本题考查了向量共线定理、向量三角形法则与平行四边形法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
20.如图是运算2+4+6+8+10的程序框图,则其中实数m的取值范围是( )
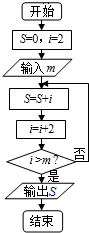

| A. | (10,12) | B. | [10,12) | C. | (10,12] | D. | [10,12] |
7.若命题p:?x∈R,x2-3x+5>0,则该命题的否定是( )
| A. | ?x∈R,x2-3x+5≤0 | B. | ?x∈R,x2-3x+5>0 | C. | ?x∈R,x2-3x+5<0 | D. | ?x∈R,x2-3x+5≤0 |
17.一个年级有20个班,每个班同学从1~50排学号,为了交流学习经验,要求每班学号为18的学生留下进行交流,这里运用的是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
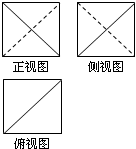 已知一个空间几何体的三视图如图所示,其三视图均为边长为1的正方形,则这个几何体的表面积为3+$\sqrt{3}$.
已知一个空间几何体的三视图如图所示,其三视图均为边长为1的正方形,则这个几何体的表面积为3+$\sqrt{3}$.